Vamos aprender como funciona a arquitetura de uma LSTM, sigla para Long Short-Term Memory, ou seja, memória de longo e curto prazo.
Essa arquitetura consegue capturar tanto o longo quanto o curto prazo, minimizando o efeito da utilização somente do curtíssimo prazo como acontece na arquitetura de uma RNN tradicional.
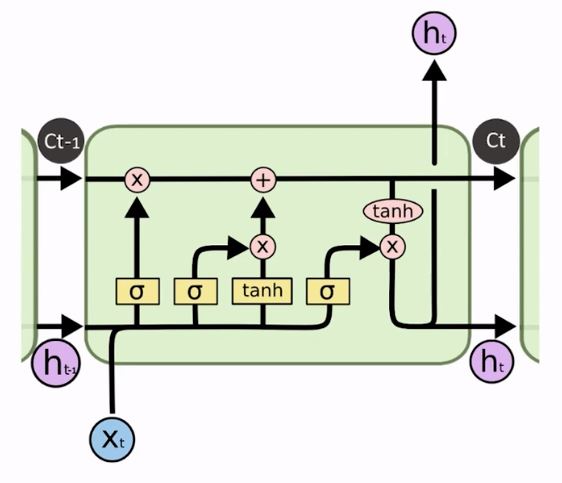
Na imagem acima já podemos ver que essa arquitetura parece mais robusta do que a de uma RNN que, basicamente, pega uma única camada de neurônios e fica realimentando-se com ela mesma.
Aqui há muito mais fluxo de informações circulando. Temos uma entrada xt, por exemplo, que passa por todo um circuito para, então, gerar um estado ht. Depois há um estado anterior ht-1, mas o que gera o próximo estado não é simplesmente uma mesma camada que está se retroalimentando.
Função sigmoide – filtro
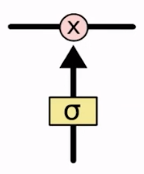
Se repararmos nesta estrutura inteira, veremos que o bloco ao lado se repete e aparece em vários lugares. Esse bloco possui uma sigmoide, que tem essa denotação justamente para indicar que é a função sigmoide.
A saída desse bloco varia entre 0 e 1 e, basicamente, pegará as entradas que estiverem passando na parte debaixo da seta, passará por uma sigmoide e a saída será algum valor entre 0 e 1. Simples assim.
Quando vemos esta bola com um x significa que será efetuada uma multiplicação: uma saída da sigmoide que será algum valor entre 0 e 1, vai multiplicar o valor que está passando nesta linha. Essa é a ideia sempre que virmos esse bloco com a multiplicação, sempre que virmos esse filtro – o quadrado com uma sigmoide – significa que é uma função sigmoide aplicada à entrada.
Então, pensando nos cálculos, podemos ver que neste caso há o estado anterior – que é o ht-1, tem a entrada xt, e esses dois estão sendo alimentados para a entrada de uma sigmoide.
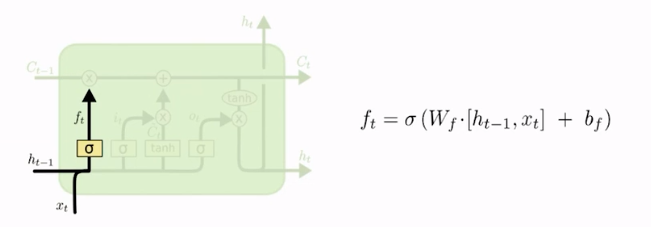
Esse bloco é simples: haverá um peso que vai multiplicar as entradas, vai somar um bias e aplicar a sigmoide em cima disso, e essa será a saída que estamos chamando de ft, que é justamente a saída da sigmoide.
A ideia desse quadro com uma sigmoide pode ser interpretada como sendo um filtro; e esse conceito será muito importante! Por que um filtro? Porque como esse dado vai multiplicar, vamos reparar que todos os locais onde aparece essa sigmoide há uma multiplicação depois. Então, na prática, se o valor que está saindo da sigmoide for igual a 1, o valor após a multiplicação fica inalterado, e assim nada mudou na saída: o filtro deixou passar tudo. Se a saída da sigmoide for 0, não importa a entrada, ela será zerada; ou seja, o filtro está barrando tudo.
Agora, se a saída for algum valor intermediário entre 0 e 1 – digamos 0,8 – quer dizer que 80% da informação está passando.
Assim, podemos interpretar a saída da sigmoide que multiplica alguma coisa como sendo um filtro que definirá o percentual da informação que ele deixará circular. Lembrando que esse percentual – o valor do filtro que será aplicado – dependerá dos parâmetros Wf e bf que serão calibrados pela rede.
Variável Ct
Chegamos então em uma etapa fundamental para uma boa compreensão: a parte de cima, onde aparece a variável chamada de Ct-1 e Ct. Da mesma forma que temos um estado anterior e o próximo estado que chamamos de h, aqui também há uma espécie de estado anterior e um próximo estado. Só que desta vez, como ele é um estado diferente, o chamamos de variável C.
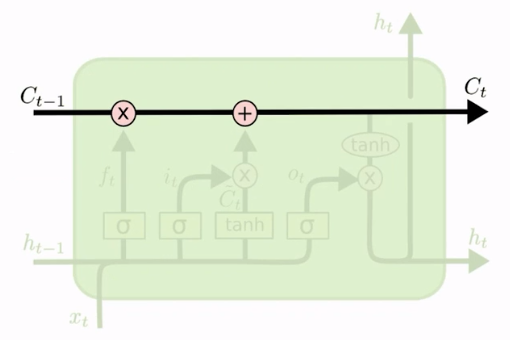
Podemos ver que Ct-1 passa por uma multiplicação que é um filtro da sigmoide que acabamos de ver; e, depois, ele segue adiante. Ele somará alguma coisa que veremos depois, e então isso se transforma no Ct.
Se formos comparar com o que acabamos de ver do nosso estudo da sigmoide, podemos ver que o Ct-1 (o estado anterior dessa variável C) é filtrado e depois disso é somado a algo e, então, gera o novo estado Ct. Então, o estado Ct sempre é acrescido do estado anterior, só que passando um filtro por ele. Podemos deduzir isso imediatamente porque vimos que esse filtro da sigmoide está passando por essa formação de Ct-1 que vai circular por cima.
Mas o que é que está sendo somado, o que gera o Ct de fato? O que gera o Ct é esse bloco em destaque abaixo:
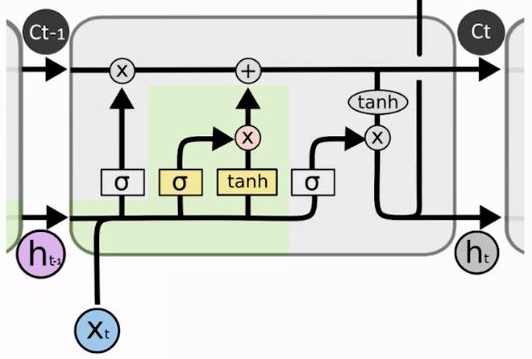
Ele recebe como entrada o xt; lembrando que a entrada xt são os nossos dados de verdade, os quais estamos tentando ajustar e descobrir para fazer as previsões. Então, a variável xt pode ser dados de ações da bolsa de valores, de um time de futebol, ou qualquer coisa que estejamos tentando prever, com as quais estamos alimentando a nossa rede. Todo o resto está sendo gerado e produzido pela própria rede.
Neste caso, na parte de baixo temos xt e temos, também, o estado anterior, ht-1, e ambos estão passando por uma função de ativação tangente hiperbólica, que é muito parecida com a sigmoide e sua diferença principal, em termos de saída, é que em vez de sair entre 0 e 1, sua saída é entre -1 e 1. Basicamente, a ideia é simplesmente essa: a partir das entradas ela definirá se a saída estará mais perto de -1 ou mais perto de 1.
Podemos, então, imaginar que temos essas entradas que estão passando para a função de ativação, e o restulado disso, em vez de ser transferido diretamente para a parte de cima da figura (somando ao Ct) será filtrada antes. Há um filtro que vai definir o quanto dessa informação, de fato, irá passar.
Cálculo de Ct
Agora, vamos parar um pouco para compreender o que está gerando a variável Ct:
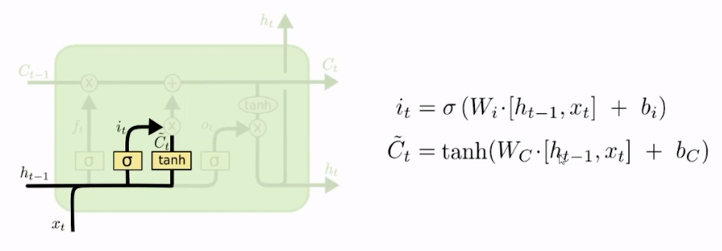
Ela é gerada a partir da entrada de xt: a entrada é que gera o estado Ct, com base na entrada do estado anterior que ainda não vimos. A entrada xt é o dado principal que está fomentando a criação do Ct a partir de uma função de ativação.
Essa entrada Ct passa por alguns pesos e bias. Ela possui pesos diferentes do que vimos anteriormente na sigmoide, apesar de estarmos usando as mesmas entradas (o filtro da sigmoide usava o ht-1 e o xt também). Como há outra função de ativação, um outro bloco, há pesos diferentes, com outra calibração.
Por isso temos um outro peso Wc*[ht-1,xt]+bc. Aqui a rede fará essa calibração para ter uma saída que será uma função dessas entradas, sendo Ct’ porque para se transformar no Ct ainda existe um filtro a ser aplicado, com a saída chamada it, que nada mais é que uma sigmoide aplicada sobre essa entrada. Assim estamos dando um novo peso usando outros parâmetros (o Wi e o bi).
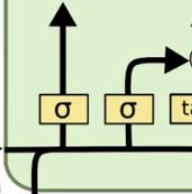Então, para facilitar a compreensão, vamos considerar os dois filtros aqui ao lado tenham resultado igual 1. Assim 100% da informação está passando por eles.
Cada novo estado Ct é gerado com base na entrada xt e na ht-1 e, depois, no próximo estado, ele será somado com o estado anterior, com o Ct-1, porque ele serve como entrada, como um input para a próxima iteração, quando haverá o próximo xt. Esse bloco se repete de novo com um novo xt, um xt+1.
A memória de longo prazo
A nossa Ct, se formos analisar ao longo do tempo, e se todos os filtros forem 1, será nada mais que uma soma do Ct-1, com o Ct-2, com o Ct-3, etc. Isso é muito relevante, porque se lembrarmos de uma rede neural recorrente, veremos que a cada novo estado, o estado anterior era diluído pela metade (que acontecia porque aquela retroalimentação estava entrando com uma nova entrada xt e o estado ht-1).
Então, sempre diluímos o estado anterior pela metade a cada nova iteração, e isto fazia com que os valores das entradas antigas fossem reduzidos muito rapidamente; depois de oito ou dez iterações, praticamente nem se considerava mais os valores das entradas antigas. Eles eram totalmente esquecidos pela rede.
Aqui não! Aqui o Ct (se os filtros estiverem saindo com valor muito próximo de 1) pode ser considerado como a memória de longo prazo, porque consiste na soma de todos os dados anteriores; eles são somados e acrescentados, sem perder valor.
É uma arquitetura que foi construída de tal forma que a memória de longo prazo está sendo preservada.
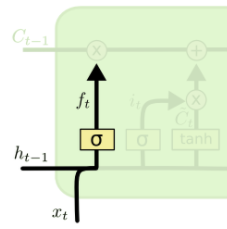E o que vai controlar a memória de longo prazo, o quanto dela vai se desvanecer? É esse filtro aqui ao lado que vai dizer o quanto da memória de longo prazo será mantida (representada pelo Ct-1).
Todo o acumulado está nesta linha que será multiplicada pelo resultado da função sigmoide; se multiplicarmos por 0,6, por exemplo, pegaremos toda a memória de longo prazo e a reduziremos por um fator de 0,6.
Então somaremos com a memória mais atual que foi recém gerada. Portanto, se a rede definir que sempre vale a pena reduzir a memória de longo prazo por um fator de 0,6, quer dizer que a memória de curto prazo terá uma relevância maior enquanto a memória de longo prazo acumulada será sempre diluída pelo fator 0,6.
O interessante aqui é que em vez de ficar sempre reduzindo cada nova iteração forçadamente com uma alta taxa como nas RNN’s, a rede LSTM terá a chance de escolher calibrar os parâmetros desse filtro de tal forma que ela definirá o que será melhor fazer.
Memória de curto prazo
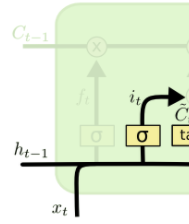Esse outro filtro aqui ao lado definirá o quanto vale a pena reduzir no dado atual, porque a rede pode perceber que o dado gerado agora, por algum motivo, passou um valor que vale a pena não reduzir e deixar passar integralmente.
Esse filtro controla o curto prazo: se vale a pena reduzir cada momento instantâneo ou não. Então temos esse ajuste fino de dois filtros controlando o curto e o longo prazo, e aí fazemos aquela alusão ao Long Short-Term Memory – memória de longo e curto prazo.
Cálculo do ht
Entendido isso, agora vamos ver a última parte do bloco, que gera o ht. O ht nada mais é que o próprio Ct que acabamos de ver, só que ele passa por uma função de ativação.
Vamos considerar que o Ct é uma memória de longo prazo (a soma das memórias anteriores, passando por alguma atenuação dos filtros) e, agora, vamos passar o resultado dessa memória de longo prazo para uma função de ativação e haverá mais um filtro aplicado sobre ele. É isso que gerará o estado ht.
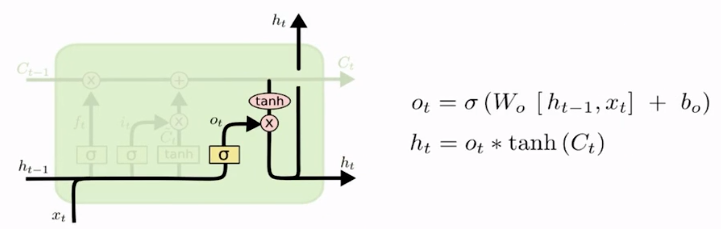
O ht nada mais é que a memória de longo prazo atenuada pelo resultado do curto prazo. Essa é a diferença do ht para o Ct: o ht é o Ct passando por uma função de ativação e por um filtro, calibrados a partir da entrada atual e do ht-1.
Se formos analisar a saída ot, ela representa a saída do filtro, ou seja, as entradas [ht-1,xt] multiplicadas pela constante Wo e somadas com bo, envolvendo tudo isso por uma sigmoide. Vamos multiplicar essa ot pela tangente hiperbólica da variável Ct.
O nosso bloco completo ficou assim:
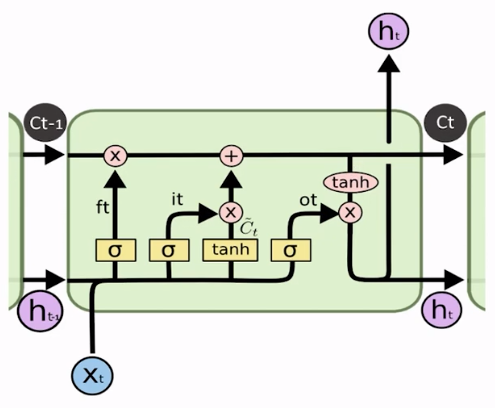
Lembrando que aquela retroalimentação que existe na RNN também acontece aqui: o Ct também é retroalimentado, só que ao invés de apenas ter a variável ht que seria atenuada para cada iteração, nós permitimos que esse fluxo de cima mantivesse o Ct puro (caso esse filtro resolva passar parte da informação).
Esse é o grande diferencial que podemos destacar, essa linha de cima:
Se não tivéssemos essa linha, teríamos um pouco mais de cálculos que seriam feitos, e no fim das contas, seria uma coisa muito parecida: os dados entrariam e gerariam um estado atual e um novo estado sendo também diluído com um xt e um ht.
Mas aqui chegamos a uma alternativa para que essa memória fosse armazenada e, com isso, tivéssemos um pouco mais de manipulação das variáveis e dos dados.
Entrada xt
Então, se formos reparar com mais detalhes, a entrada xt é um conjunto de neurônios. Aqui ilustramos apenas como uma bola, dando a impressão de que é um dado somente, porém poremos trabalhar com vários dados (várias variáveis preditoras). Por exemplo, podemos entrar aqui com dez valores ao mesmo tempo: dez neurônios como entrada.
Na prática, se formos analisar a dimensionalidade da nossa rede, essa entrada xt vai multiplicar uma camada inicial, uma camada densa de neurônios, e aí teremos uma multiplicação de parâmetros – os pesos w que serão usados por todas as sigmoides – que são calculadas com base numa camada densa que multiplicou a entrada xt.
No resultado desses valores, a saída da tangente hiperbólica que foi aplicada em cima desse vetor de neurônios teve que multiplicar o filtro; então, se ela teve uma multiplicação valor a valor, ponto a ponto com ele, eles têm que ter a mesma dimensão.
Analisando em destalhes veremos que todas essas saídas (ft, it, ot, Ct) têm a mesma dimensionalidade. Na realidade, a dimensionalidade da rede inteira e todas as saídas dela são definidas por uma camada só de neurônios que definiremos.
Então, quando formos programar uma LSTM, basta que informemos quantos neurônios queremos na nossa rede e definiremos quantos neurônios vão multiplicar a nossa camada de entrada para gerar as primeiras variáveis e, a partir disso, gerar todos esses estados Ct e ht e gerar todo o fluxo dessa LSTM, como vimos.
Como aprender mais sobre LSTMs na prática?
Este e outros assuntos são abordados de maneira detalhada (teoria e prática) em nosso curso Módulo 4 de Machine Learning e Deep Learning. Focamos sempre na didática para que todos tenham um aprendizado completo. É um curso imperdível sobre o que há de mais avançado no mundo do deep learning. Aproveite!
Outros artigos relacionados:
- Como funcionam as Redes Neurais Recorrentes
- Redes Neurais em Problemas de Regressão
- Empilhando LSTM em camadas
- O que é Processamento de Linguagem Natural (NLP)
- Como funcionam os sistemas de tradução
- Introdução a GAN’s – Redes Adversárias Generativas
- Frameworks para deep learning
- Quando utilizar GPU para Deep Learning
- Dominando o TensorFlow
