O Transposed Convolutional Layer aumenta o tamanho de uma imagem, usando a técnica de convolução.
O conceito de convolução que nós vimos no artigo Introdução a Redes Neurais Convolucionais é, basicamente, um filtro (de convolução) com um tamanho específico, que vai varrendo uma imagem original com seu deslocamento, o que faz com que ele tente capturar uma característica específica na imagem e, com isso, formar um feature map.
Esse feature map pode ser interpretado como uma imagem também gerada a partir da imagem original. Essa imagem do feature map fica com uma dimensão menor do que a imagem original.
Inclusive há uma fórmula para calcular qual será a dimensão final desse feature map, a partir dos parâmetros do filtro escolhido. Esses parâmetros podem ser o kernel, que é tamanho do filtro que usamos, com a letra k (pode ser, por exemplo, 3×3, 5×5); o padding, ou seja, se a imagem terá bordas de zeros antes de aplicar a convolução (por exemplo, podemos colocar uma ou mais camadas de zeros na borda da imagem) – isto seria a letra p que usamos; e, também, podemos usar o stride, que seria esse deslocamento representado pela letra s.
Esses três parâmetros (o padding, o stride e o tamanho do filtro – o kernel) são o que determinam, depois, qual será o tamanho final da nossa imagem resultante, o qual acaba sempre sendo menor do que a imagem original.
Com isso, quanto mais filtros (mais camadas de convolução) vamos fazendo, vai diminuindo cada vez mais o tamanho da imagem resultante, até que ela fique com um tamanho bem menor do que o tamanho que ela se originou.
Podemos, também, usar vários filtros em cada camada; então, de uma camada para outra podemos ter 60 filtros, por exemplo; depois, a próxima camada pode ter 100 filtros. Mas todos os filtros da mesma camada têm o mesmo objetivo, todos eles varrem a imagem anterior. Esse é o conceito de convolução que já abordamos!
A convolução no Transposed Convolutional Layer
A ideia de Transposed Convolutional Layer que veremos agora, trabalha de forma muito semelhante e, também faz uma convolução, mas de uma forma quase como se fosse o seu oposto.
Isto porque ela também varrerá a imagem, só que a imagem resultante terá uma dimensão maior que a imagem original. Enquanto o Convolutional Layer vai diminuindo o tamanho da imagem, o Transposed Convolutional Layer vai aumentando o tamanho da imagem a cada camada de convolução adicionada. Como isto vai funcionar?
Funcionamento
Basicamente, o Transposed Convolutional Layer também receberá os três parâmetros (o padding, o tamanho do kernel e o tamanho do stride que será feito), só que o resultado desse Transposed Convolutional Layer vai definir dois outros parâmetros: o parâmetro z, que adiciona zeros entre os pixels, e parâmetro p’, que dirá quantas bordas de zeros nós vamos adicionar na imagem final.
Parâmetro z
Vamos imaginar que a nossa imagem tenha uma determinada quantidade de pixels; por exemplo, cada neurônio dessa imagem é um pixel de uma cor específica (os quadradinhos), e queremos adicionar uma camada de zeros entre as linhas.
Se fôssemos colocar uma camada de zeros entre cada uma das linhas da figura, ficaria conforme abaixo:
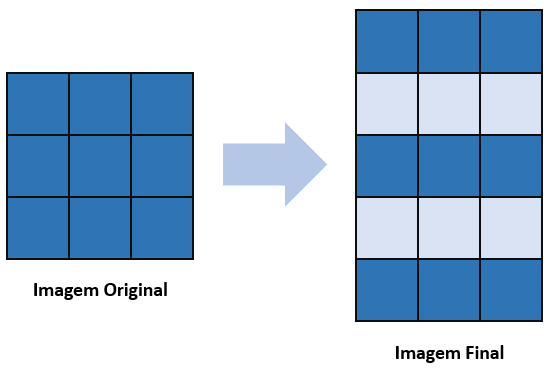
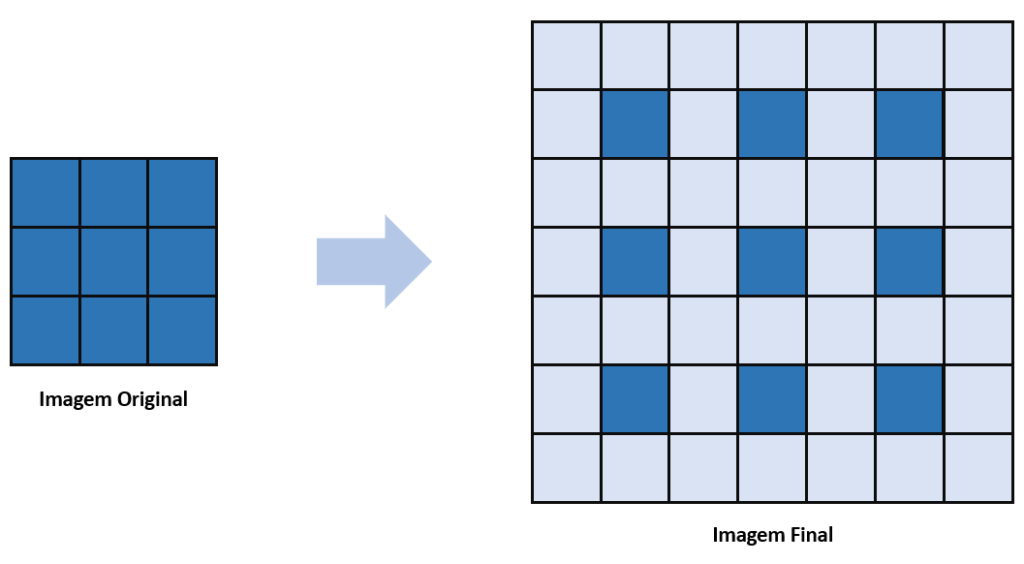
No parâmetro z, quando dizemos, por exemplo, que z = 1, quer dizer que adicionaremos uma camada de zeros tanto nas linhas quanto nas colunas; então, o resultado da imagem ficará assim:
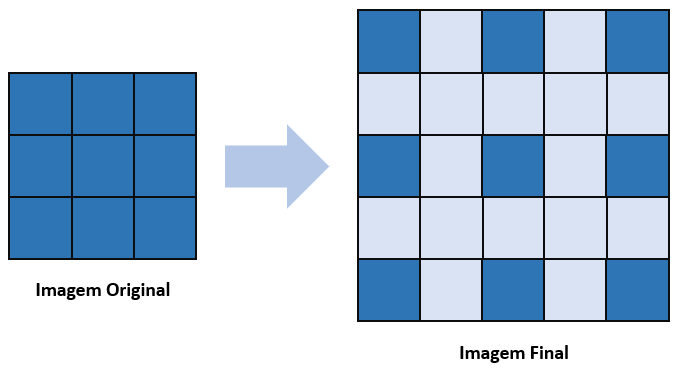
Fica claro que a imagem acaba ficando maior, aumentada em termos de tamanho graças a essa técnica de aplicar zeros entre cada um dos pixels. Se colocamos um z igual a 2 ou 3, são mais camadas intermediárias que estarão entre os pixels das linhas e das colunas.
Parâmetro p’
No parâmetro p’ teremos uma grande diferença em relação à convolução: enquanto no padding da convolução nós adicionávamos uma borda de zeros na imagem antes de aplicar o filtro de convolução, aqui no Transposed Convolutional Layer nós colocaremos essa borda de zeros na imagem final.
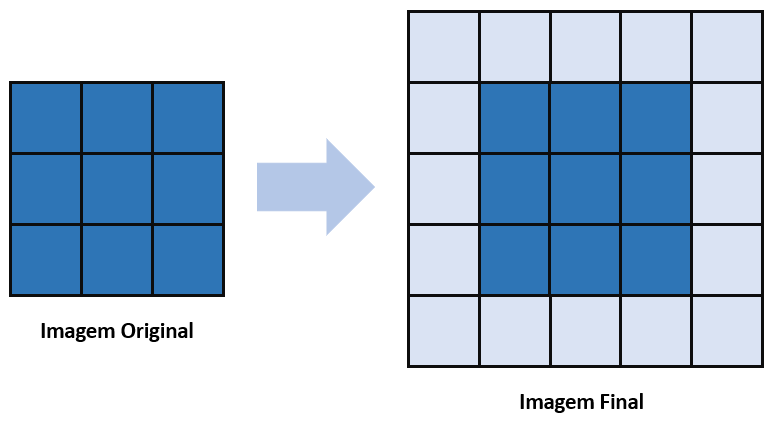
Então, nós já varremos a imagem, já ficamos com ela em tamanho reduzido devido ao filtro de convolução que passou por ela, e agora nessa imagem resultante colocaremos zeros em sua borda para que ela aumente o seu tamanho.
A imagem final terá zeros na sua borda. Esse é o p’ que estamos falando aqui, que vai na imagem resultante; enquanto o p é na imagem original. Essa é a diferença do Transposed Convolutional Layer para a camada de convolução normal como nós já conhecemos.
Resultado
Esses parâmetros do p’ e do z podem ser calculados a partir de algumas fórmulas: o z pode ser calculado como sendo z = s – 1, ou seja, nós informamos qual é o stride e ele calcula qual será o tamanho do z final. O p’ pode ser calculado como p’ = k – p – 1, ou seja, depende do tamanho do kernel e do tamanho do padding.
Com isso podemos imaginar como ficará nossa imagem final de saída:

Informamos os parâmetros k, p e s, que será o filtro que varrerá a imagem (só que a imagem resultante criará esses dois parâmetros: o p’ e o z, que aumentarão o resultado). Então, fizemos essa convolução, e o que geraria um resultado menor acaba gerando um resultado maior – uma imagem maior – porque adicionamos várias camadas de zeros entre os pixels da imagem, tanto na borda como entre cada um dos pixels.
Isso, por enquanto, pode parecer meio abstrato e podemos perguntar o porquê de se fazer assim, qual o objetivo em aumentar o tamanho de uma imagem?
Até onde podemos observar não estamos melhorando a resolução da imagem, estamos apenas adicionando pixels zeros para que a dimensão dela fique maior. Não adicionamos qualidade na imagem, pois quem vai adicioná-la será a técnica Generative Adversarial Networks.
Nessa técnica teremos duas redes neurais trabalhando uma contra a outra e será isso o que fará com que a qualidade da imagem melhore. Mas, depois, conhecendo toda a arquitetura do modelo, é possível se entender o porquê precisamos, num desses modelos, ficar aumentando a dimensão da imagem.
Na realidade, começaremos com o ruído e, a partir dele, vamos transformá-lo numa imagem, aumentando cada vez mais a sua dimensão até que ele fique na dimensão da imagem que queremos imitar.
Arquitetura do modelo
Conforme mencionamos, entender a arquitetura do modelo é algo fundamental, e que envolverá algumas etapas. Em nosso curso Aprendizado por Reforço, Algoritmos Genéticos, NLP e GANs abordamos cada uma dessas etapas, de maneira simples e objetiva, com foco na didática, para que todos tenham um aprendizado completo.
Confira também todos os nossos cursos, temos opções do básico ao avançado.
Leia também:
