Como funciona o Gradiente Descendente Estocástico

Você já ouviu falar de Gradiente Descendente Estocástico? Apesar deste nome assustar, o conceito, na verdade, é muito simples de ser compreendido. Ele é muito aplicado na área das Redes neurais e Deep learning.

Devido à grande importância e utilidade que esse assunto tem, gostaríamos de dar um panorama sobre ele.

Antes de prosseguir, gostaríamos de sugerir que, se você ainda não conhece o que é Gradiente Descendente, você assista este vídeo. Assim, você poderá compreender melhor os conceitos aqui explicados. Bons estudos!

Os Gradientes Descendentes e a Função Custo

Quando estamos atualizando os pesos de uma rede neural, a partir de uma função de custo, o que esta função faz é comparar a previsão que a nossa rede neural está fazendo – a classificação que ela está tendo – com o resultado real – o gabarito.

Após, medimos o tamanho do erro e tentamos minimizar a soma dos erros. Essa função nada mais é do que a soma de todos os erros; e o nosso objetivo é minimizar esses erros, de forma que a Rede Neural fique cada vez mais precisa.

Vamos supor que estejamos treinando uma rede neural com uma série de imagens, 10 mil, por exemplo. Nesse caso, nós poderíamos atualizar todos os pesos da rede neural com base somente em uma imagem.

Esse cenário não seria o ideal, pois faria com que a rede ficasse viciada: ela aprenderia muito bem como reconhecer aquela imagem específica; mas talvez não fosse uma rede que generalizasse muito bem, se entrássemos com outra imagem, talvez ela não saberia classificá-la.

Portanto, o ideal seria atualizar os pesos numa iteração com base em todas as imagens de entrada. Ou seja, estaríamos somando os erros para cada uma das imagens – cada uma das amostras – e a partir dessa soma total é que tentaríamos reduzir a função de custo – não somente em relação a uma imagem.

Isso gera, no entanto, um custo computacional elevado.

Nosso exemplo de 10 mil imagens já parece grande, mas se analisarmos casos de big data – que tem um conjunto de dados muito maior – esse custo computacional aumenta de forma brutal, pois quanto maior é o nosso conjunto de dados de treinamento, maior é o custo associado.

Dessa forma, o método de Gradiente Descendente pode ser muito prejudicado, o que faz com que as atualizações sejam muito lentas. Talvez até se consiga chegar em um modelo bem calibrado; mas levará muito tempo para que se consiga fazer a rede neural chegar a esse ponto.

Barra de carregamento - processamento lento

Também é possível que o nosso computador nem consiga fazer isso; ele pode simplesmente travar porque atingiu o limite de memória.

Parte de uma conjunto de dados de imagens

Como podemos, então, tentar contornar esse problema do custo computacional? É aí que entra o Gradiente Descendente Estocástico.

Em vez de pagar todo o conjunto de dados, ele pega somente uma parte desses dados para fazer cada atualização dos pesos.

Obviamente não estaremos usando somente uma imagem, pois já comentamos que isso deixaria o modelo muito enviesado, mas por que não utilizar um número como 200 imagens para cada atualização?

Se, em cada atualização dos pesos da rede neural, estivermos passando um grupo de imagens diferente e genérico o bastante, talvez o algoritmo esteja caminhando na direção certa em direção ao ponto ótimo da função de custo.

Obs: não confunda função de custo com custo computacional. Custo computacional é o gasto com o computador que vai ficar ligado processando. Função de custo é a soma de todos os erros gerados pelo modelo ao comparar as previsões feitas pelo modelo e os valores reais.

Aplicação prática com a função custo

Para compreendermos um pouco melhor como o Gradiente Descendente Estocástico funciona, voltemos à função de custo.

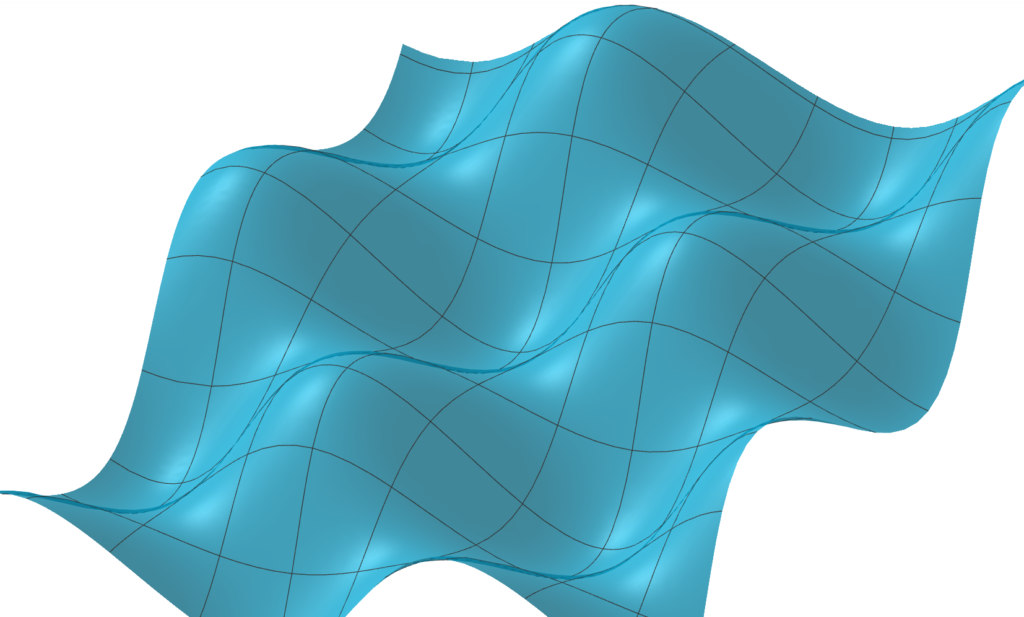
Gráfico de uma função de custos em três dimensões

Estamos vendo o gráfico que poderia representar a função de custos usando três dimensões. Vamos imaginar que a função de custo tenha, a partir das variáveis, pontos que sejam mais altos e pontos mais baixos.

Ou seja, estamos interessados nos pontos em que a função de custo seja menor – queremos chegar naqueles pontos; atualizando nossos pesos de maneira que o algoritmo descubra qual é o ponto mais baixo dessa função.

Por começarmos aleatoriamente, é provável que acabemos começando em um ponto não ideal, no qual a função de custo estaria bem longe do vale. Nesse caso, caminharemos em direção aos pontos em que a função de custo seja menor.

Cada vez que fazemos uma atualização dos pesos da nossa rede neural usando o método de Gradiente Descendente – que é uma derivada –, estamos indo na direção do mínimo da função.

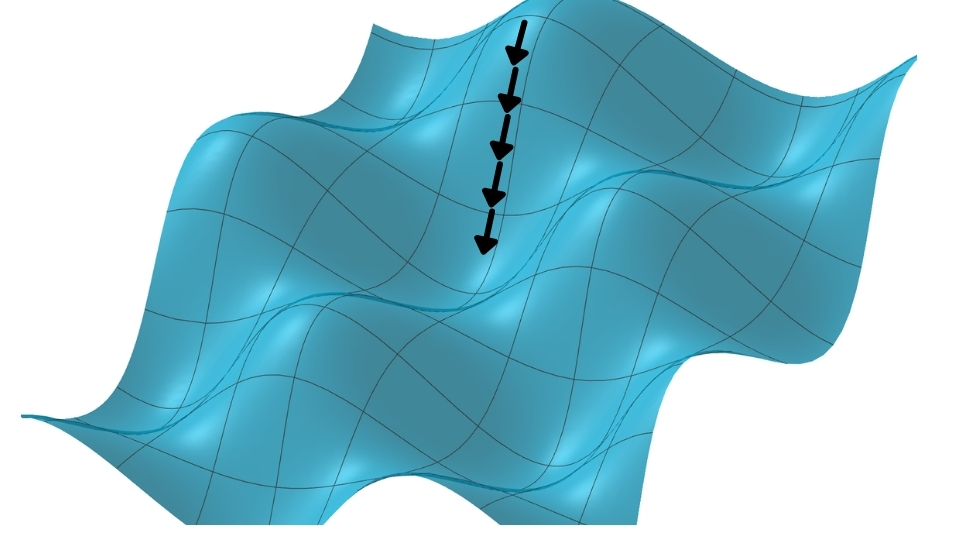
Iterações em direção ao mínimo da função custo

Cada vez que fazemos uma iteração, nós damos um passo em direção ao mínimo – essas “flechinhas” que aparecem no gráfico, cada uma delas representa uma iteração; a cada iteração nós damos um pequeno passo. Estamos cada vez mais perto do nosso objetivo.

Quando utilizamos todas as imagens (10 mil, em nosso exemplo) para avaliar o erro e dar um passo, estaremos dando o passo mais otimizado possível, que é o que foi visto no gráfico.

Podemos, por outro lado, escolher utilizar somente uma parte do conjunto de dados. Ao invés de 10 mil amostras, atualizaríamos os pesos com base em 200 amostras, por exemplo; nessa situação, somaríamos o custo para 200 imagens diferentes.

O que aconteceria com o nosso Gradiente Descendente nesse caso? Provavelmente não daríamos um passo na direção mais otimizada possível.

Como estaríamos utilizando apenas uma parte das amostras, daríamos um passo que vai, sim, na direção de minimizar a função total; no entanto, esse passo não será o mais otimizado, afinal, não estaríamos analisando todas as amostras.

Podemos imaginar que faríamos isso de forma repetitiva, sempre com um conjunto novo de amostras. Isso faria com que os passos do nosso Gradiente Descendente ficassem um pouco mais tortos – como se fosse um bêbado caminhando.

Por isso, a expressão “o andar de um bêbado” é bastante usada em relação ao Gradiente Descendente Estocástico. Em casos como esse, as atualizações dos pesos da rede neural não são feitas da forma mais otimizada possível.

Dessa maneira, não estaríamos andando na direção de máxima variação em direção ao mínimo da função: por não utilizarmos todas as amostras (todo o conjunto de dados), estaríamos andando de forma cambaleante; nosso caminho não seria perfeito, mas seria na direção certa – mesmo que lentamente.

Ao selecionarmos uma pequena amostra do total, nós temos um indício de onde temos que ir, ainda que não saibamos exatamente o valor exato de onde temos que ir.

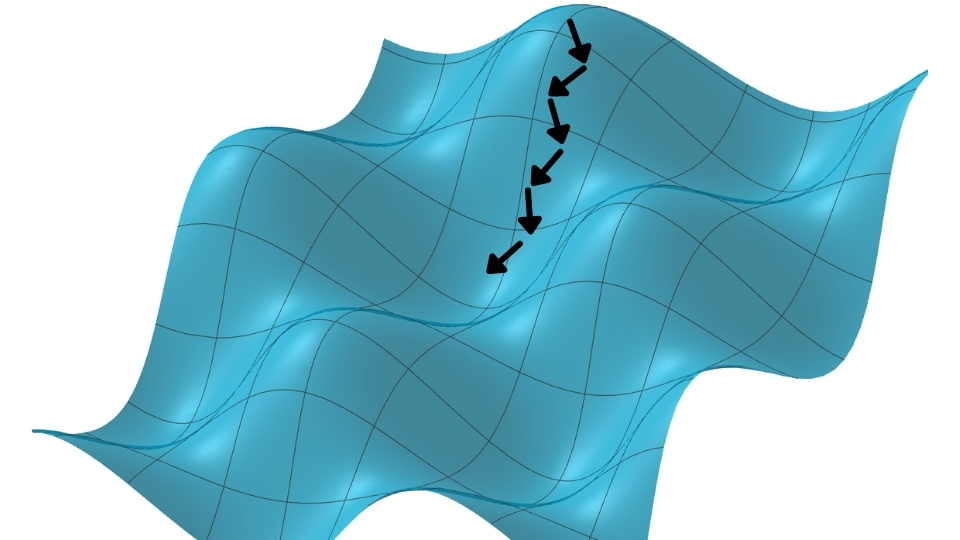
Representação gráfica do "andar de um bêbado" do Gradiente Descendente estocástico

Olhando dessa forma, a situação pode parecer meio contra intuitiva: nós estamos fazendo algo que não seria o melhor possível; pela lógica, o ideal seria caminharmos na direção exata de onde temos que ir, mas como já comentamos, o custo computacional também é relevante.

No Gradiente Estocástico, cada passo é muito rápido – estaríamos usando apenas 200 amostras ao invés de usarmos as 10 mil.

Ainda que envolva mais passos cambaleantes, o Gradiente Estocástico é muito mais rápido no fim das contas.

No exemplo do nosso segundo gráfico, o treinamento da rede neural acaba sendo muito mais rápido do que o anterior; nós acabamos chegando praticamente no mesmo lugar de uma forma muito mais rápida – ainda que um pouco mais torto e com um pouco mais de iterações. Isso acaba sendo uma grande vantagem, especialmente se precisarmos aumentar o conjunto de dados.

Se o nosso problema possui 100 mil, 1 milhão, ou ainda 10 milhões de amostras, podemos sempre utilizar apenas uma pequena parte do conjunto para a fazer a nossa atualização do Gradiente Descendente Estocástico – o que diminui o tempo do processo.

Escolhendo a quantidade ideal de amostras

A quantidade de amostras utilizada para cada iteração é chamada de mini-batch e ela é definida previamente: 500, 200, 100, 30, 1000 amostras, não importa.

Nós escolhemos o tamanho do lote que vamos usar na programação; definido o tamanho, não importa se o nosso conjunto de dados tem uma quantidade muito grande de amostras, ele sempre usará aquele tamanho específico de mini-batch para fazer cada uma das atualizações.

O mini-batch é, então, um dos fatores que vamos variar quando estivermos usando a programação das redes neurais. Podemos escolher diferentes tamanhos. Surge, entretanto, um questionamento: qual será o trade off em relação ao tamanho de mini-batch escolhido?

Fica evidente que, quanto maior o tamanho do mini-batch que escolhemos, mais preciso será o caminhar do nosso Gradiente Descendente.

Quanto maior esse conjunto de amostras, entretanto, mais tempo o Gradiente levará para fazer a atualização dos pesos. Por outro lado, quanto menor o mini-batch, ainda que menos preciso, mais rápido será o Gradiente. Devemos avaliar o custo-benefício.

Pessoa avaliando o custo benefício

Pode ser que, ao utilizar um lote pequeno, cheguemos mais rápido a uma performance muito boa. Ou pode ser que a performance final fique ruim – ainda que rápida; ou seja, o gradiente não conseguiu chegar em lugar nenhum – ele ficou tão “bêbado” que não conseguiu ir na direção de mínimo.

Em um caso como esse, nós poderíamos aumentar um pouco o tamanho do minibatch para que sua performance melhore.

Agora, entendendo esse conceito, saiba que há diferentes tipos de gradiente descendente estocástico, cada qual com sua peculiaridade. Todos tem como objetivo fazer os passos de forma menos “bêbada” possível. Por exemplo, podemos usar médias móveis para fazer com que o caminhar do Gradiente seja mais suave.

Essas diferentes ideias e aplicações deram origem aos algoritmos Adam, RMSprop, ADAdelta, entre outros.

Como aprender mais

Agora que você já conhece mais sobre Gradiente Descendente Estocástico, talvez queira continuar aprendendo. Para isso, nós recomendamos que você aprofunde seus conhecimentos de matemática. Aqui você encontra opções gratuitas que irão lhe ajudar muito:

Para quem realmente quer aprender machine learning e deep learning, conheça nosso curso completo de redes neurais e deep learning. Nesse curso você vai aprender inteligência artificial, matemática e programação ao mesmo tempo, com muita eficiência e didática.

Conheça todos os nossos cursos e potencialize seu aprendizado hoje mesmo.