Vamos aprender sobre os conceitos de variância e de viés, pois eles são muito importantes no estudo de Machine Learning. Talvez você já conheça os conceitos de underfitting e overfitting.
Se esse é seu caso, você verá que eles andam lado a lado com os conceitos de variância e de viés.
Se ainda não conhece, leia o artigo lincado acima, pois compreender esses termos é uma das bases para o aprendizado de algoritmos de machine learning.
Entendendo o viés
Para compreendermos melhor o que é viés, vamos analisar o conjunto de dados abaixo:
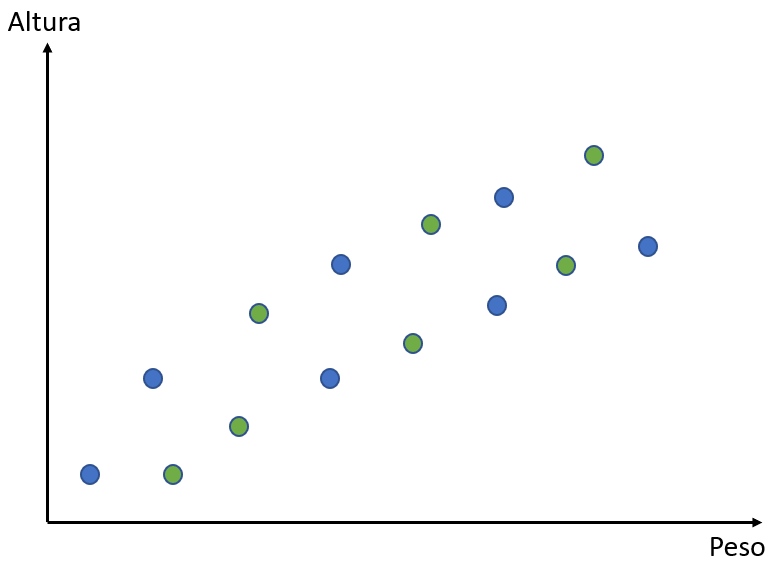
Nesse gráfico, os pontos azuis e verdes mostram os dados de altura e peso de um certo número de pessoas. O nosso objetivo, nesse caso, será tentar construir um modelo que melhor se adeque aos dados e consiga prevê-los.
Com esse modelo, esperamos conseguir determinar o peso de alguém a partir de sua altura e vice-versa. Para criarmos esse modelo, primeiramente vamos dividir os nossos dados em dois conjuntos: dados de treino e dados de teste. Selecionamos, então, aleatoriamente, alguns desses dados para construirmos nosso modelo; os pontos verdes serão os dados que usaremos para treino; nós construiremos nosso modelo só com base nesses pontos.
Com o modelo pronto, iremos testá-lo com os pontos azuis para vermos se ele chega a um bom resultado. Nessa lógica, os pontos azuis servirão como dados de teste.
Imaginemos, agora, que temos dois algoritmos diferentes para gerar modelos para esse conjunto de dados. O algoritmo que vamos chamar de Modelo 1 tentará simplesmente traçar uma reta que melhor descreva o comportamento dos dados. Confira abaixo:
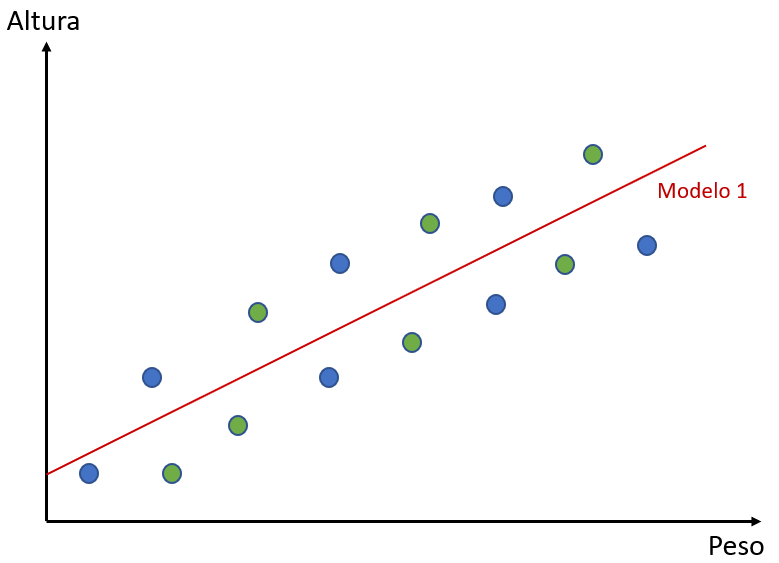
Esse modelo se utilizou dos pontos verdes e construiu a reta que melhor se adequou a eles. O outro algoritmo, que chamaremos Modelo 2, também tentará se adequar melhor aos pontos verdes. Entretanto, ele não fará isso com uma reta. Confira:
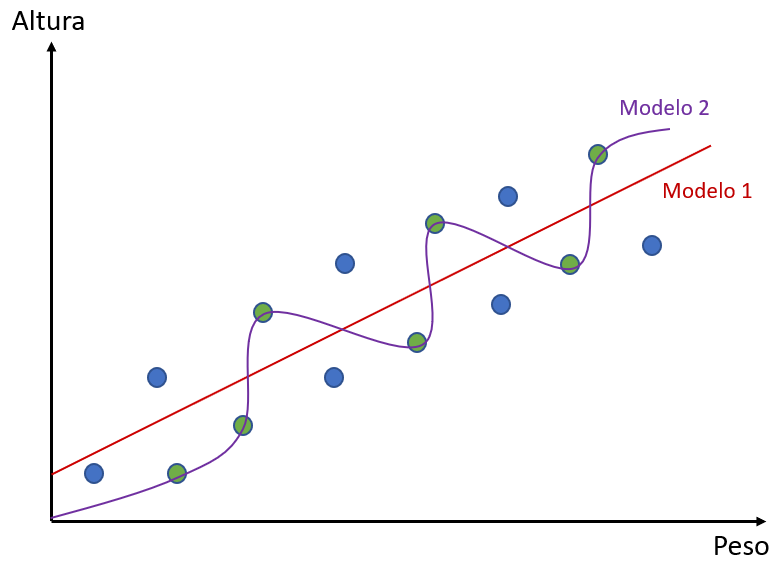
O que seria, então, viés? O conceito de viés, se aplica a flexibilidade de um modelo. Pensando em relação aos dados de treino, quando um modelo é mais flexível em relação aos dados – quando ele procura passar bem perto deles –, ele é considerado um modelo com baixo viés.
Em relação ao nosso exemplo, podemos dizer que o Modelo 2 tem um baixo viés, enquanto o Modelo 1 tem um alto viés. Por quê? Porque o modelo 1 não é um modelo muito flexível: ele não está passando tão próximo dos dados quanto o modelo 2. O Modelo 2 se adequa aos dados de forma melhor que o Modelo 1. Quanto mais um modelo se adequa aos dados menor o seu viés.
Entendendo a variância
Agora que entendemos o conceito de viés, podemos passar para a variância. A variância diz respeito ao quão generalista o nosso modelo é. Ou seja, em relação aos dados de teste, quanto erro ele produz.
A variância perguntará o seguinte: quanto erro o Modelo 1 ou o Modelo 2 produzem em ralação aos dados de teste? Lembrando que no nosso conjunto de dados os dados de teste são representados pelo pontos azuis.
Para saber o erro dos dados de teste, pegamos cada um dos pontos e calculamos a distância desse ponto para cada uma das linhas – a reta do Modelo 1 ou as curvas do Modelo 2.
Abaixo você pode ver a representação da distância de um dos pontos de cada modelo. Note que as retas de distância estão separadas para que se possa vê-las. Na realidade, entretanto, elas sairiam do mesmo ponto e chegariam ao mesmo ponto no gráfico, ficando sobrepostas.
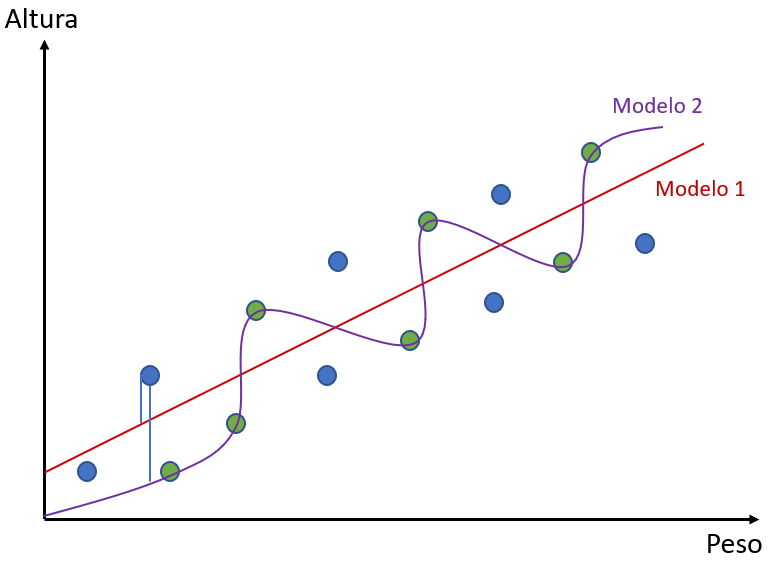
Lembre-se que cada coordenada do gráfico representa um peso e uma altura. Dessa forma, a partir de um valor de peso, cada algoritmo dará um valor de altura correspondente. Assim, podemos ver que para cada ponto dos dados de teste, cada modelo dará um resultado diferente.
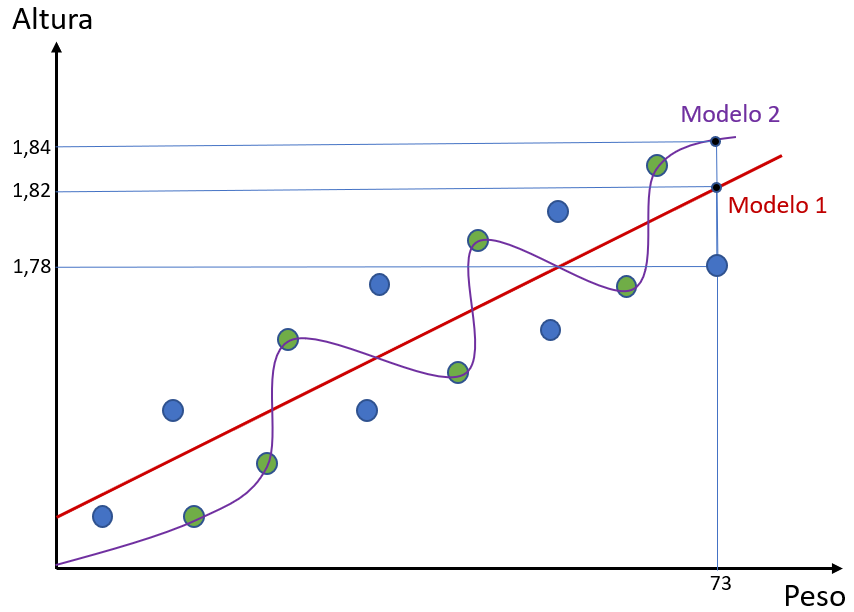
Agora podemos ver como cada modelo se comportou na previsão dos valores. Vamos supor que tenhamos um ponto com peso 73kg (os valores são para fins didáticos e não estão em escala).
É possível perceber que, para tal ponto, o Modelo 1 previu uma altura de 1,82m e o Modelo 2 uma altura de 1,84m. Cada algoritmo irá dar uma previsão diferente pois eles foram modelados de formas diferente.
Entretanto, o valor real da altura do ponto era de 1,78m. Ou seja, há um erro associado. Se calcularmos as distâncias de todos os pontos em relação aos modelos, nós teremos o erro total de cada modelo.
Considerando isso, vemos que o Modelo 2 está com um erro maior que o Modelo 1 para os nossos pontos azuis – nossos pontos de teste. No exemplo que utilizamos, o erro do Modelo 1 foi 0,04 para mais, enquanto o erro do Modelo 2 foi de 0,06 para mais.
E isso pode ser percebido ao longo de todo gráfico com os outros pontos. Como o Modelo 2 teve um erro maior, nós dizemos que ele teve uma variância maior. Assim, dizemos que quanto maior o erro, maior a variância.
Unindo os conceitos
Resumindo o que vimos até o momento: a variância nos diz qual é o erro de um modelo em relação aos dados de teste; o viés, por outro lado, nos diz o quão bem um modelo se adequa aos dados de treino.
Qual seria, então, o modelo ideal? Seria aquele modelo que tem um baixo viés e uma baixa variância. Ou seja, um algoritmo que se adequa muito bem aos dados e que erra muito pouco.
Dessa forma, temos um modelo mais generalista possível, um modelo que consegue, para um conjunto de dados desconhecido, não ficar tão preso só aos dados de treino.
Se analisarmos o nosso Modelo 2, constataremos que ele está muito preso aos dados e treino não modelando bem os dados de teste. Nesse caso, dizemos que esse modelo está sofrendo de overfitting.
Por outro lado, é possível dizer que o Modelo 1 está sofrendo de underfitting; ele está sendo muito generalista e não está capturando bem a relação peso x altura. O modelo tentou fazer uma relação linear.
O peso e a altura, entretanto, não são exatamente lineares. Abaixo, você pode ver uma representação de um modelo ideal. Para o caso dos nossos dados, ele não seria linear (como o caso do Modelo 1), nem seria tão específico (como o caso do Modelo 2).
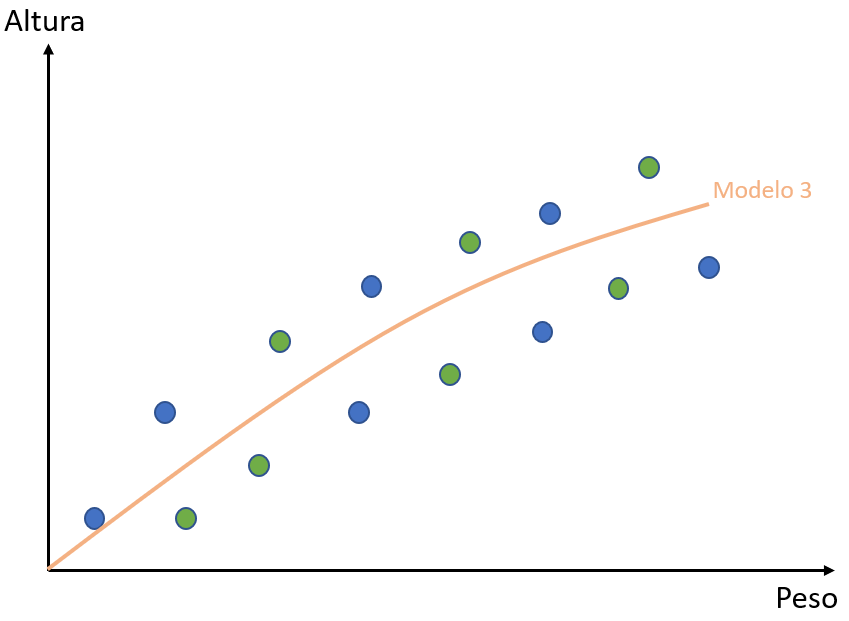
Agora que você conhece bem os conceitos, você pode dizer que esse modelo tem um viés baixo (tem certa flexibilidade) e tem uma baixa variância (consegue generalizar bem os dados).
Esse algoritmo conseguiria um bom resultado tanto com os dados de treino quanto com os dados de teste. É exatamente isso que nós buscamos, porque de nada nos adianta ter um bom resultado só com os dados de treino e não ter um bom resultado com os dados de teste.
Continue aprendendo
Neste artigo, você leu sobre conceitos que são essenciais para o aprendizado de machine learning e inteligência artificial. Com isso em mente, nós queremos incentivar você a continuar aprofundando seus conhecimentos nessas áreas, que vem tendo cada vez mais relevância hoje em dia.
E você pode continuar fazendo isso aqui no Didática Tech. Confira nossos cursos completos de machine learning! Temos diversas opções tanto pagas quanto gratuitas que serão úteis em seu aprendizado, sempre focando na didática e absorção do conteúdo.
Leia também outros artigos:
