Neste artigo, nós vamos desmistificar a probabilidade. Muitos sentem até calafrios quando ouvem essa palavra; mas você verá que no final, esse não é um conceito complicado para ser compreendido.
Nosso objetivo aqui é mostrar algumas ideias básicas e fundamentais sobre esse assunto tão importante na matemática.
Começando da base em questões de probabilística, avançando para outros assuntos, tudo ficará mais fácil. Além disso, ao longo de seu aprendizado de machine learning e inteligência artificial, você verá que compreender a probabilidade é fundamental.
O que é probabilidade?
A primeira coisa que precisamos entender é que probabilidade é a chance de algo acontecer. Se falamos que há uma probabilidade de 10%, por exemplo, é a mesma coisa que dizer que há uma probabilidade de 10 sobre 100, porque é dez por cento.
Isso significa que temos UMA chance em DEZ de algo ocorrer. Além disso, também podemos representar como 1 sobre 10, ou um décimo.
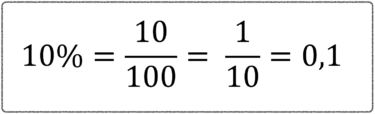
 Para explicar de forma bem simples, imagine que você tem uma caixa com 10 frutas. Dessas 10 frutas, 9 são laranjas e 1 é maça. Se você fechar os olhos e retirar uma fruta da caixa, qual a chance de você retirar a maçã?
Para explicar de forma bem simples, imagine que você tem uma caixa com 10 frutas. Dessas 10 frutas, 9 são laranjas e 1 é maça. Se você fechar os olhos e retirar uma fruta da caixa, qual a chance de você retirar a maçã?
É uma chance em 10, pois temos uma maçã no meio de 10 frutas. Assim, dizemos que a probabilidade de se retirar a maçã é de 10%.
Resolvendo problemas de probabilidade
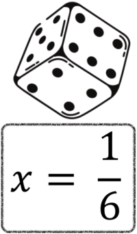
Vamos, então, começar a resolver alguns problemas simples de probabilidade. Imagine que você tenha um dado com seis números de 1 a 6. Sabemos que, se jogamos um dado, há a mesma chance de cair cada número.
Ou seja, todos os números têm a mesma probabilidade de serem sorteados. Nesse caso, qual é a probabilidade de cair o número 4, por exemplo?
Como faríamos essa conta? A conta a ser feita é a seguinte: queremos que saia um número 4, que aparece só uma vez no dado. Quantas faces (ou números) o dado tem? Seis.
Então, a chance de aparecer o número 4 é UMA (pois só há UM número 4) em SEIS possibilidades (porque podem sair SEIS números). É bem simples: temos seis números e queremos que saia um, então é uma chance em seis: 1/6.
Agora, se perguntarmos qual a chance de sair o número 4 OU o número 5? Agora já temos duas chances, porque são dois números que podem sair de seis.
O 2 vai para o numerador (em cima) e o seis para o denominador (embaixo).
Nesse segundo exemplo a probabilidade seria de 2/6.
Podemos, ainda, simplificar dividindo o numerador e o denominador por 2 e ficaria 1/3. Analisando esses dois exemplos, podemos dizer que o segundo é mais provável de acontecer, pois 1/3 é maior que 1/6.
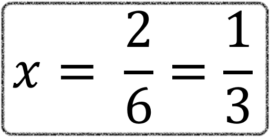
Em resumo, a fórmula da probabilidade é a seguinte: a chance do evento que queremos dividida pelas chances totais de possibilidades.
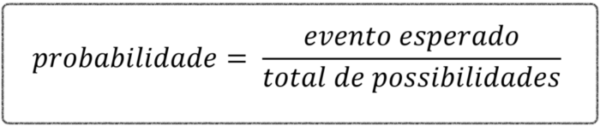
Vamos agora, então, aumentar um pouco a dificuldade fazendo a seguinte pergunta: Se fizermos dois lançamentos de dados, qual a chance de sair o número 4 duas vezes repetidas?
Sabemos que para sair uma vez somente é 1/6. Entretanto, vamos jogar uma segunda vez e queremos que saia, de novo, o número 4.
Quando queremos que um mesmo evento se repita consecutivamente iremos multiplicar as probabilidades.
Nós sabemos que cada evento tem a probabilidade de 1/6 de ocorrer. Iremos, assim, multiplicar 1/6 por 1/6, obtendo o resultado de 1/36.
Ou seja, a probabilidade de tirarmos o número quatro DUAS vezes é de 1/36.
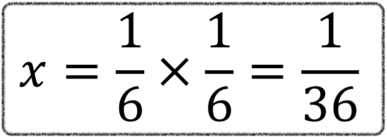
Essa, é uma chance bem mais difícil de ocorrer do que as anteriores, pois 1/36 é um número muito pequeno. Quando acumulamos eventos, é mais difícil de eles ocorrerem.
Nessa lógica, se quiséssemos três eventos, multiplicaríamos por 1/6 mais uma vez. Isso deixaria o numerador maior e, por consequência, a probabilidade menor ainda.
Qual a chance de algo não ocorrer?
Em um próximo estágio, nós podemos tentar descobrir a chance de algo não acontecer. Vamos imaginar que o problema, agora, é o seguinte: qual é a chance de não sair o número 4 quando jogarmos o dado?
Iremos considerar A como a chance de um evento ocorrer e N como a chance de o mesmo evento não ocorrer. A chance de acontecer um evento, mais a chance de não acontecer será sempre igual a um: A + N = 1.
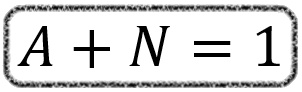
O que isso significa na prática? Vamos pensar sobre o evento que acabamos de perguntar: qual a chance de não sair o número 4 quando um dado é jogado?
Nesse caso, queremos descobrir o valor de N. Para isso, podemos isolá-lo da seguinte maneira: N = 1 – A.
Nós já sabemos a chance de acontecer o evento A, que é 1/6. Então, a chance de não acontecer será N = 1 – 1/6. Um menos um sexto são cinco sextos (N = 1 – 1/6 = 5/6).
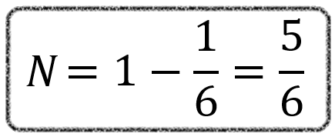
É claro que poderíamos ter chegado a essa resposta de outra forma: a chance de não ocorrer o número 4 é a chance de ocorrer qualquer um dos outros números do dado. Há cinco números que podem sair além do 4 (1,2,3,5,6).
Ou seja, são CINCO números num espaço de possibilidades de SEIS números (5/6). Entretanto, apresentamos a fórmula A + N = 1 pois ela será muito útil para uma série de outros problemas.
Aumentando a dificuldade
A pergunta agora será a seguinte: se jogarmos o dado duas vezes, qual a chance de sair o número 4 ao menos uma vez? É muito comum que pessoas formulem essa resposta de forma errada.
Qual seria uma maneira errada de se pensar? Seria a seguinte: Sabemos que a chance de acontecer uma vez é 1/6 (se jogarmos uma vez o dado, não há dúvidas de que a chance de sair o número 4 é 1/6); mas jogaremos duas vezes.
Quando jogarmos de novo, a chance também será 1/6; ora, então se jogarmos duas vezes a chance total de sair o número 4 será 1/6 mais 1/6, que dá 2/6 ou 1/3 (1/6 + 1/6 = 2/6 = 1/3).
Isso até parece lógico: vamos jogar uma vez e temos um sexto de chance (1/6), depois jogamos mais uma vez e teremos mais um sexto de chance (1/6), então dará dois sextos (2/6). Entretanto, isso está errado!
Temos que tomar muito cuidado quando formos somar probabilidades, pois a chance de estarmos calculando algo errado é muito grande.
Raramente devemos somar uma probabilidade em eventos que vamos repetir. Por quê?
Vamos utilizar um exemplo para esclarecer. Pela lógica utilizada acima, se jogássemos o dado sete vezes, a probabilidade de cair o número 4 seria 1/6 x 7 = 7/6.
Ou seja, teríamos mais do que 100% de chance do evento ocorrer, o que é impossível.
Além disso, uma probabilidade de 100% representa a certeza de que algo irá ocorrer. No entanto, se jogamos um dado 7 vezes, é bem possível que o número 4 não caia nenhuma vez.
Aqui vale uma dica, antes de resolver um problema de probabilidade, pense um pouco, tente imaginar outros cenários e hipóteses diferentes para ver se os resultados irão fazer sentido na realidade.
Às vezes, testando um pouco, descobrimos que a nossa metodologia de resolução está errada, como aconteceu nesse exemplo.
Qual seria, então, o jeito certo de resolver o problema? Seria utilizar a fórmula que apresentamos antes: a chance de acontecer mais a chance de não acontecer é igual a um (A + N = 1).
Relembrando: queremos que, jogando o dado duas vezes, saia o número 4 pelo menos uma vez. Anteriormente, nós tentamos trabalhar com o A, somando duas vezes a chance de um número quatro sair. Agora, vamos tentar trabalhar com o N para ver se funciona.
Qual é a chance de não cair o número 4 em dois lançamentos? A chance de não acontecer em um lançamento já vimos que é 5/6; para não acontecer em dois lançamentos, nós devemos multiplicar esse valor por ele mesmo. Isso será a chance de os eventos não ocorrerem.
Ou seja, nosso N será 5/6 x 5/6. Lembre-se do exemplo de lançamentos consecutivos que utilizamos no início do artigo.
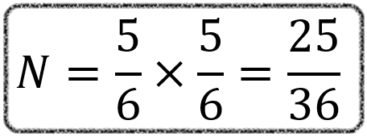
Agora fica fácil calcular a chance de o evento acontecer. É só aplicar a fórmula: A = 1 – 25/36. Essa será a probabilidade do número 4 cair em pelo menos um de dois lançamentos. Se resolvermos isso com a calculadora, chegaremos no resultado de 0,3 mais ou menos.
Lembrando que também podemos dizer que a chance é de 30%.
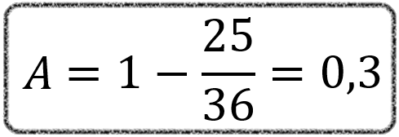
Se quiséssemos mais lançamentos, como 3 por exemplo, seria só multiplicar o N por ele mesmo mais uma vez. Poderíamos dizer que queremos que o número 4 saia pelo menos uma vez em três lançamentos.
Ora, vamos pensar assim: a chance de sair em três lançamentos é 1 menos a chance de não sair nos três lançamentos. Qual é a chance de não sair nos três lançamentos? Será 5/6 x 5/ x 5/6.
Depois é só aplicar na fórmula como já vimos. Se pensarmos dessa forma, tudo ficará mais simples! Sempre que houver um problema de probabilidade e não soubermos como fazer, podemos tentar pensar no contrário, tentar pensar na chance de não acontecer aquele evento.
Caso você queira ver o conteúdo deste artigo em formato de vídeo, acompanhe a aula abaixo:
Aprenda mais
Nosso intuito aqui foi apresentar alguns conceitos básicos de probabilidade. Agora, recomendamos que você continue aprofundando seus conhecimentos sobre matemática e machine learning. Para isso, temos dois cursos gratuitos que irão te ajudar:
Além disso, aqui temos diversos outros cursos que você pode conferir. Temos opções tanto pagas quanto gratuitas, todas com muita didática e exemplos práticos focados no aprendizado do aluno. Clique aqui e aproveite.
Leia também outros artigos:
