Como funciona o algoritmo de Bagging? (Machine Learning)

O algoritmo de Bagging tem como principal função tentar evitar o overfitting. Ele faz isso construindo vários estimadores, usando o mesmo modelo várias vezes para, depois, fazer uma média somando esses modelos individuais, conforme o agrupamento existente nos Métodos Ensemble.

Definição do modelo

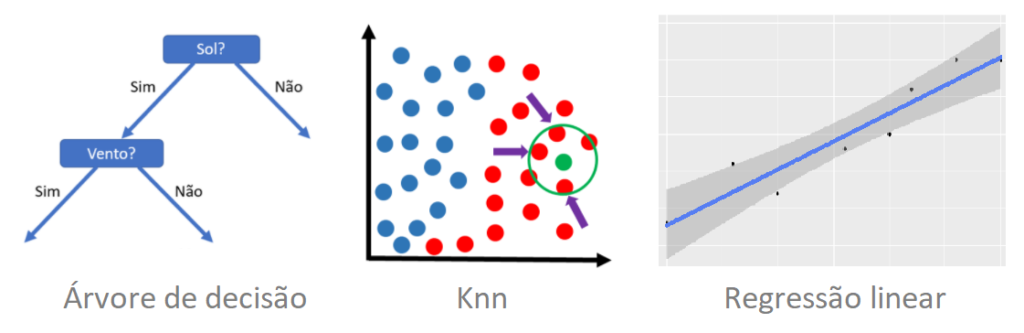
A primeira coisa a ser feita com este algoritmo é escolher qual o modelo que será usado. Por exemplo, podemos optar pelo algoritmo de árvore de decisão, ou KNN, ou Regressão Linear; enfim, um algoritmo de machine learning que será o padrão para o algoritmo de Bagging funcionar.

Então, ao escolher o Árvore de decisão, por exemplo, passando esse parâmetro para o algoritmo de Bagging, ele construirá várias vezes esse algoritmo.

Exemplos de algoritmos para Bagging: árvore de decisão, knn e regressão linear

Vamos imaginar que temos um conjunto de dados que o algoritmo de Bagging pegará para rodar a primeira árvore de decisão; depois ele construirá a segunda árvore de decisão, a terceira, e assim por diante, de acordo com o número de árvores que pedimos para serem construídas.

Por fim, ele utilizará os resultados individuais de cada árvore para, através da média desses valores, apresentar seu resultado final.

Pensando dessa forma, pode parecer que não faz muito sentido. Isto por que se ele fizer isso com o conjunto de dados que lhe foi informado, basicamente construirá dez estimadores iguais (se esse foi o número que pedimos) porque ele usará o mesmo algoritmo.

Quando nós vimos o Random Forest ou o Extratrees, por exemplo, eles construíram vários estimadores, sendo que cada um com características diferentes: eles usavam a aleatoriedade para construir cada um dos estimadores.

Se for construído um estimador com base nos mesmos dados, simplesmente, e depois apenas refletir isso, terá sido construído, basicamente, o mesmo estimador várias vezes. Então, a média desses estimadores será, nada além do resultado de um estimador só.

Escolha aleatória das amostras

Então o que o Bagging usa para fazer uma diferenciação entre um estimador e outro, sendo que ele está usando o mesmo algoritmo? No caso das árvores de decisão, qual a diferença entre uma árvore e outra?

Dado - escolha aleatória das amostras O Bagging faz uma escolha aleatória das amostras. Para fazer a primeira árvore de decisão, ele escolhe um conjunto específico de amostras, sorteando algumas do conjunto total de dados. Com esse dataset ele escolhe cinco mil amostras de um total de dez mil, por exemplo, para a construção da árvore.

Se quisermos, podemos pedir que ele escolha 50 % do nosso conjunto de dados, para cada estimador. Então, a primeira árvore de decisão será montada com base em 50% das amostras, sendo que a escolha será aleatória.

Ou seja, cada árvore será construída com base em cinco mil amostras de um total de dez mil, e cada amostra dessas cinco mil, terá sido sorteada aleatoriamente.

Explicando detalhadamente, o processo se dá assim: o Bagging faz um sorteio de todas as amostras; escolhe uma e, depois, faz outro sorteio e escolhe a segunda; e, dessa forma, ele segue sorteando as cinco mil amostras.

Destas, algumas podem vir duplicadas ou repetidas; ou seja, ele usa o bootstrapping para fazer repetições. Assim ele forma o dataset que constrói a primeira árvore de decisão. A segunda árvore passa a ser construída da mesma forma: através de um novo sorteio de cinco mil amostras. Para cada estimador, ele faz uma árvore diferente, porque ele trabalha com conjuntos de dados diferentes.

Aqui, haverá amostras que não serão as mesmas da próxima; cada uma será um pouco diferente, com critérios diferentes; isto, porque, ele se baseou num conjunto diferente para a construção de cada uma.

É dessa forma que o Bagging consegue construir estimadores diferentes: ele usa o mesmo algoritmo, só que para cada estimador, criado separadamente, ele usa um conjunto diferente de amostras.

Essa é a técnica, a fórmula usada pelo Bagging para diferenciar um estimador de outro. E esse mesmo processo acontece com cada algoritmo, não apenas com árvore de decisão.

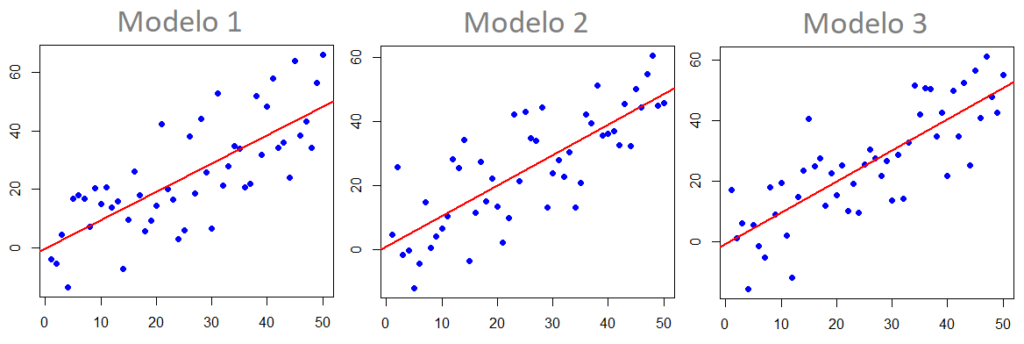
Se tivéssemos escolhido Regressão Linear, por exemplo, ele faria a mesma coisa, construiria vários estimadores com conjuntos de amostras diferentes.

Diferentes retas de regressão linear feitas pelo bagging

Aqui poderíamos lembrar do Random Forest, porque ele faz justamente isto. Ou seja, para construir a primeira árvore de decisão, ele escolhe aleatoriamente uma parte do conjunto de amostras, que costuma ser dois terços do conjunto total.

É claro que ele faz algumas coisas extras: escolhe aleatoriamente algumas variáveis, dentre vários fenômenos randômicos para formar cada uma das árvores. O algoritmo de Random Forest usa Bagging naturalmente, construindo apenas árvores de decisão.

Classificação e Regressão

Em problemas de classificação, se escolhe qual o algoritmo base para classificação; e se for um problema de regressão, se escolhe qual o algoritmo base de regressão. A técnica usada é basicamente a mesma: ele sorteará randomicamente as amostras, um percentual delas, com bootstrapping (a reamostragem) porque algumas podem vir repetidas e, a partir daí, construirá cada um dos estimadores para separá-los.

A quantidade será informada assim: se forem dez estimadores, ele fará dez vezes o processo, e usará a média; sendo que o resultado será nosso escore final.

Problemas de Classificação: o resultado de cada estimador será uma base, e a que for mais abundante na votação individual dos estimadores, será a classe definida como resultado final.

Problemas de Regressão: o algoritmo fará a média dos resultados de cada um dos estimadores.

Evitando o overfitting

O interessante no algoritmo de Bagging é a sua estratégia, sua estrutura para evitar o overfitting.

A forma como ele o evita é justamente tentando construir diferentes estimadores a partir de diferentes conjuntos de dados, de forma que a construção de um estimador só não fique enviesada.

Se escolhêssemos um só algoritmo para o nosso problema, o de regressão logística, por exemplo, ele sempre teria este problema, tentando ficar muito próximo dos dados de treino, porque se fez um ajuste muito fixo para estes dados, e depois, ao se apresentar os dados de teste, ele não se forma tão bem por conta do enviesamento dos dados de treino.

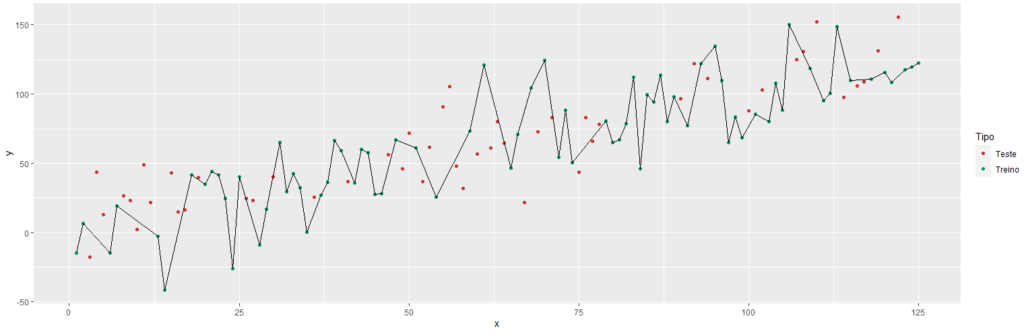
Qualquer algoritmo de machine learning tem esse problema, e o Bagging tenta evitá-lo construindo algoritmos que não fiquem muito ajustados aos dados de treino.

Ele constrói o primeiro estimador, que não se ajusta perfeitamente a todo o conjunto de dados de treino. Isto, porque, ele já escolheu algumas amostras de forma aleatória.

Depois ele faz um outro estimador que será ligeiramente diferente do primeiro e um terceiro que também será diferente dos anteriores. Então, assim se constroem vários estimadores que usam critérios diferentes.

Generalizando

Quando se entra com um novo conjunto de dados, a tendência é que este estimador final, que faz um agrupamento, agregue os resultados de vários estimadores individuais, usando um resultado não enviesado.

Isto acontece em razão da mistura, fazendo uma combinação muito diferente entre os dados de entrada, e conseguindo generalizar bem pois não está “tão preocupado” com os dados de treino, nem em passar por cada um dos seus resultados, evitando uma análise viciada nos dados de treino.

Modelo sem overfitting aplicado aos dados de treino — Modelo generalizável aplicado nos dados de treino

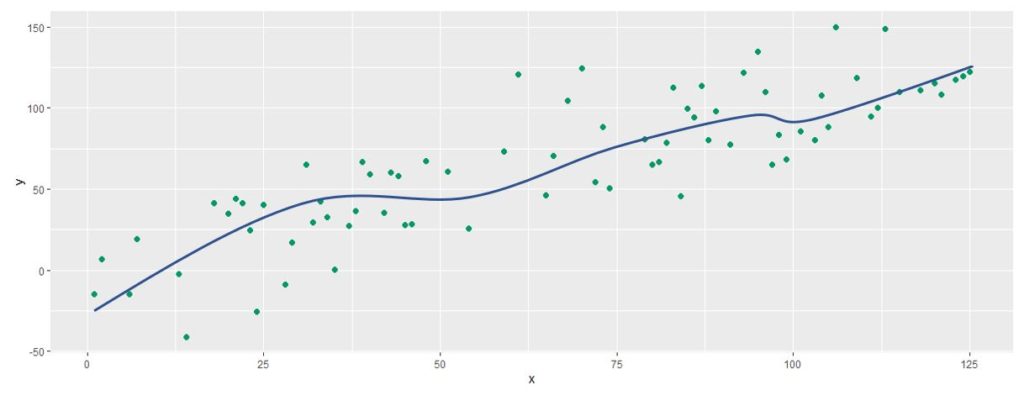
Ele generalizou, pegou apenas um conjunto aleatório, depois formou outro, e outro, e outro; criando, assim, vários estimadores diferentes. Agora, trazendo os dados de treino, quando entrar com um conjunto de dados, ele já teria uma performance que não seria perfeita nos dados de treino, porque ele construiu cada estimador com base numa amostragem aleatória daqueles dados.

E ele já não será perfeito na amostragem de treino, o que é bom! É bom porque significa que quando ele entrar com dados de teste, a performance será “parecida”, como se fosse com novos estimadores de treino.

Essa é a forma principal de trabalho do Bagging com o overfitting.

Modelo sem overfitting aplicado aos dados de teste — Modelo generalizável aplicado nos dados de teste

Aplicar esta técnica na prática nos ajuda a entender que uma das principais formas de se aumentar a performance de um algoritmo é justamente fazendo com que ele fique generalizável.

É necessário que isto entre em nossa mente, pois temos uma forte tendência em pensar que quanto mais complexo for o algoritmo, melhor ele conseguirá se adequar aos dados, ou mais poderoso ele será.

Na realidade, entretanto, na maioria das vezes, o segredo da boa performance é ter um algoritmo que não se prenda muito aos valores de treino, e não fique muito enviesado a eles. Queremos que ele consiga generalizar bem, sem se preocupar com as informações de treino, apegando-se somente à essência principal dos dados, sem ir muito a fundo neles.

Esses algoritmos são os que performam melhor, porque conseguem dar resultados bem genéricos; e a técnica de Bagging ilustra isso muito bem, pois pega um algoritmo já conhecido, e a única coisa diferente que ele faz é sortear aleatoriamente as amostras.

Só isso já tem uma capacidade de generalização muito forte, o que faz com que sua performance melhore bastante.

Bagging na prática

Em nossos cursos de Machine Learning vemos em detalhes tanto teoria, quanto prática, criando modelos em linguagem R e Python. Com foco no aprendizado do aluno, abordamos os conceitos necessários de maneira objetiva e com muita didática.

Ensinamos e utilizamos na prática o algoritmo Bagging no módulo 2 de machine learning. Confira!