Regressão linear é o método com o qual se encontra a reta que melhor descreve a relação entre os dados. A reta é criada com uma equação linear y = b + m1*x1…mn*xn, onde b será o coeficiente linear, e m o coeficiente angular, sendo um para cada variável preditora existente nos dados.
Função lm()
Nesse artigo, iremos focar na criação de retas de regressão linear no R, utilizando a função lm(), que torna este processo muito simples e prático.
Para encontrarmos os valores de m e b na linguagem R, basta passarmos os valores das variáveis para a função lm(). A notação utilizada é a seguinte: lm(variável target ~ variáveis preditoras). Sempre passaremos apenas uma variável target, e poderemos passar uma ou mais variáveis preditoras.
Vamos considerar que temos os pesos e alturas de algumas pessoas, e precisamos encontrar a reta que melhor descreve a relação entre essas duas variáveis.
> peso <- c(45,50,60,55,58,56,48,53)
> altura <- c(1.54,1.56,1.65,1.60,1.65,1.63,1.58,1.59)
> plot(peso, altura)
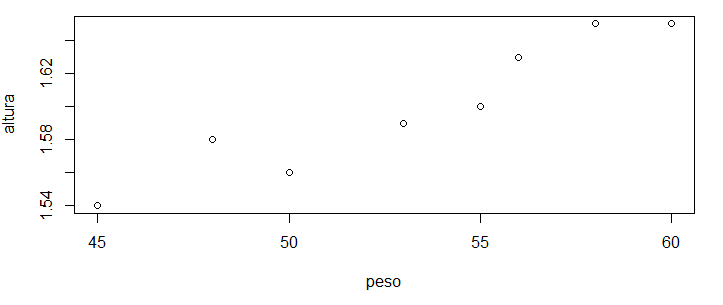
Podemos ver na imagem acima que, conforme o peso aumenta, a altura também aumenta, deixando clara a relação entre os dados. Se esse gráfico estivesse em um papel, poderíamos facilmente desenhar uma reta no meio dos pontos.
Mas sem os valores exatos do coeficiente linear e angular, a reta não estaria precisa, sendo apenas uma aproximação da reta ideal.
> lm(altura ~ peso)
Call:
lm(formula = altura ~ peso)
Coefficients:
(Intercept) peso
1.200575 0.007519
Com o código lm(altura ~ peso), os valores das variáveis são passados para a função, indicando que buscamos a reta que explica a variação na altura das pessoas, em função dos seus respectivos pesos.
Como resposta recebemos o valor “Intercept”, que é o coeficiente linear, e o coeficiente angular é apresentado junto a sua respectiva variável, no caso a peso. Com estes valores podemos facilmente inserir a reta exata no gráfico.
> abline(1.200575, 0.007519)
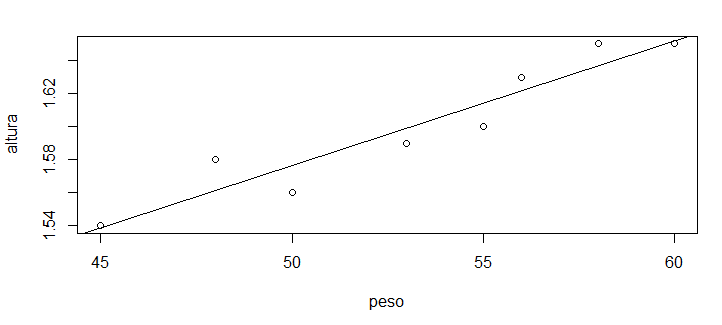
Uma vez que já plotamos o gráfico anterior, podemos realizar inserções nele. Com a função abline() inserimos uma reta, e passamos como parâmetros os valores do coeficientes obtidos através da função lm().
Teríamos o mesmo resultado executando diretamente a função abline(lm(altura ~ peso)), não sendo necessário copiar e colar os valores.
ggplot2
Aqueles que não conhecem a linguagem R podem estar olhando esses gráficos sem muita empolgação, achando o visual deles muito simples. Isso acontece pois criamos as plotagens sem especificar nenhuma parâmetro.
Mesmo nas funções do pacote base, como plot() e abline(), existem muitos parâmetros que podem ser configurados para melhorar a apresentação do gráfico, mas uma forma ainda mais simples de se obter boas visualizações na linguagem R é através do pacote ggplot2.
> library(ggplot2)
> ggplot(mapping = aes(peso, altura)) +
geom_point() +
geom_smooth(method = "lm")
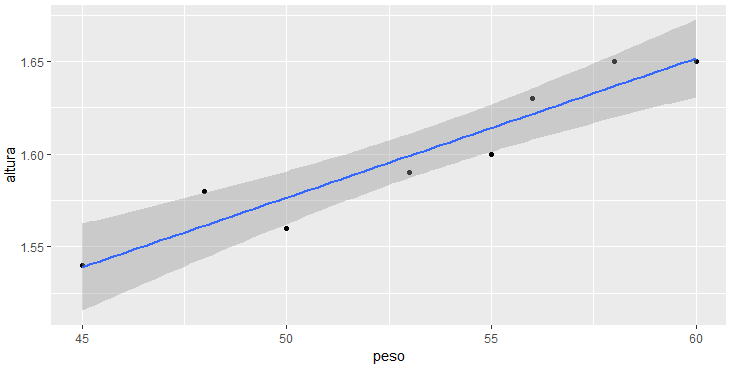
Percebam que novamente não passamos nenhum ajuste visual ao gráfico, utilizando assim o padrão do ggplot2. Porém esta visualização padrão já é consideravelmente mais agradável, e ainda pode ser customizada com muitos ajustes.
Coeficiente de determinação R2
Por mais que a reta esteja bem ajustada aos pontos no gráfico, podemos ver que ela não é perfeita, ou seja, ela não passa por todos os pontos. Na realidade, ela não passa por nenhum deles. Isto acontece devido a relação existente entre os dados, que não possui uma proporção direta.
Não há uma regra que estabeleça que a cada quilo a mais, a pessoa terá um centímetro a mais, por exemplo. Este comportamento é normal, levando à necessidade de avaliarmos a reta criada, sendo uma das alternativas para essa finalidade o coeficiente de determinação R2.
Esse coeficiente compara a reta em questão com uma reta gerada a partir da simples média dos dados. Cada erro da reta média é elevado ao quadrado para então serem todos somados.
O mesmo cálculo é feito com a reta de regressão. O erro total da reta média é subtraído pelo erro total da reta de regressão, e o resultado dividido pelo erro da reta média. Desta forma, o resultado nos mostra o quão melhor a reta de regressão é diante da reta média. Vamos entender melhor:
> retas <- ggplot(mapping = aes(peso, altura)) +
geom_point() +
geom_smooth(se = FALSE, method = "lm") +
geom_hline(yintercept = mean(altura))
> retas
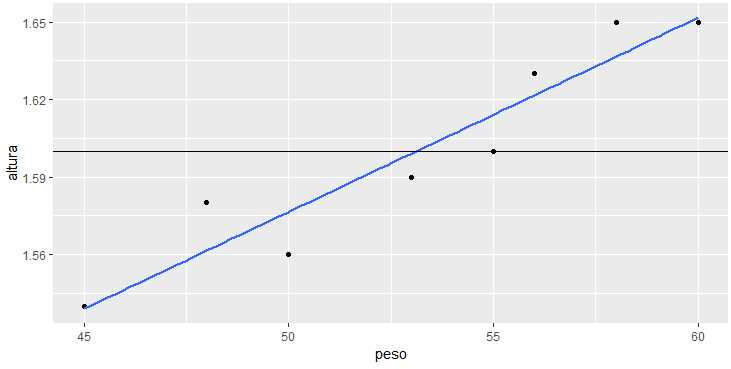
Neste gráfico inserimos a reta média, que é calculada através da média dos valores de y (que no caso é 1.6) e tem coeficiente angular igual a zero, gerando assim uma reta paralela ao eixo x, cruzando o eixo y no ponto 1.6. Agora podemos visualizar os erros da reta média.
> retas +
geom_segment(aes(x = peso, y = altura,
xend = peso, yend = mean(altura)), color="red")
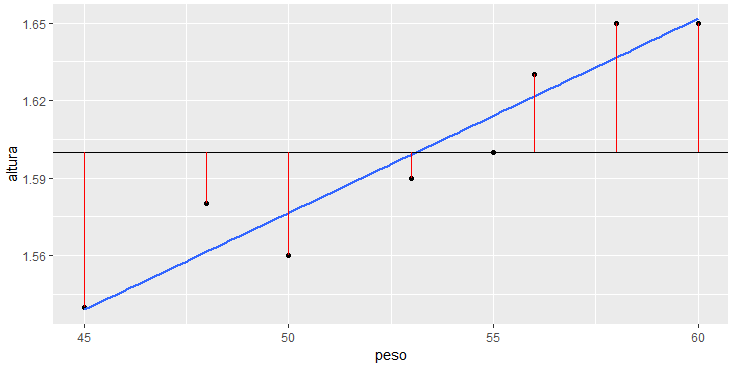
Acima vemos em vermelho a distância entre o valor real da altura de uma pessoa para o valor informado pela reta média. Por exemplo, a pessoa com peso igual a 50 tem altura igual a 1.56, porém a reta indica 1.6, sendo o erro 0.04, que é o tamanho da distância em vermelho.
Todos os erros, apresentados em vermelho no gráfico, serão elevados ao quadrado e então somados, levando a soma dos quadrados dos erros da reta média, que iremos chamar de SQt.
> retas +
geom_segment(aes(x = peso, y = altura,
xend = peso, yend = predict(lm(altura ~ peso))), color="red")
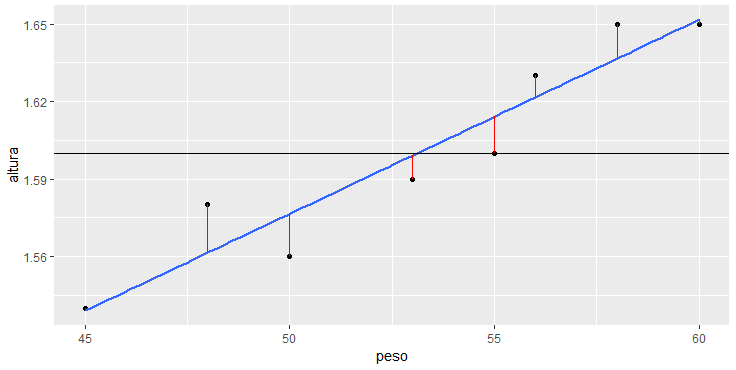
O mesmo processo acontece com a reta de regressão linear, que também tem seus erros representados pelas distâncias em vermelho. Chegamos assim a soma dos quadrados dos erros da reta de regressão, que chamaremos de SQres. Calculando SQt e SQres encontraremos o R2.
SQt = sum((mean(altura) - altura)**2)
SQres = sum((predict(lm(altura ~ peso)) - altura)**2)
R2 = (SQt - SQres) / SQt
R2
0.9009349
Assim chegamos ao valor do coeficiente de determinação R2 neste exemplo, que é igual a 0.9009, ou 90,09%. Podemos dizer que a reta de regressão linear y = 1.200575 + 0.007519 * x, é 90,09% melhor do que a reta média y = 1.6 + 0 * x, para expressar a relação entre o peso destas pessoas, e suas alturas.
Função summary()
Para entendermos bem o conceito do coeficiente de determinação R2, realizamos este detalhamento, porém ao utilizar a função lm() o processo apresentado não é necessário. Com a função summary() podemos obter resumos na linguagem R, o que se aplica também a objetos criados através da função lm().
> summary(lm(altura ~ peso))
Call:
lm(formula = altura ~ peso)
Residuals:
Min 1Q Median 3Q Max
-0.0165044 -0.0103195 -0.0003009 0.0096247 0.0185328
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.200575 0.054293 22.113 5.59e-07 ***
peso 0.007519 0.001018 7.387 0.000316 ***
Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.01384 on 6 degrees of freedom
Multiple R-squared: 0.9009, Adjusted R-squared: 0.8844
F-statistic: 54.57 on 1 and 6 DF, p-value: 0.0003158
Passando como parâmetro para função summary(), a regressão linear criada com a função lm(), o resultado acima é apresentado, com muitos detalhes sobre a regressão.
Um destes detalhes é o coeficiente de determinação R2, que é apresentado como “Multiple R-squared:”, e podemos verificar que o seu valor é igual ao que calculamos anteriormente.
Regressão linear para machine learning
Assim concluímos que a reta de regressão apresentada é a melhor reta que poderia ser traçada para descrever a variação da altura em função do peso. Sabendo disso, podemos utilizar essa reta para prever novas alturas.
Olhando para a reta, vemos que se tivermos uma nova pessoa com peso igual a 50, a reta indica que essa pessoa tem uma altura de aproximadamente 1,58. Substituindo o valor de x na equação por 50, teremos o valor exato que essa reta está indicando: altura = 1.200575 + 50 * 0.007519, altura = 1,576525.
Essa é uma das formas de aplicação da regressão linear no machine learning, para previsão de valores futuros ou desconhecidos. Assim, utilizamos a reta de regressão linear criada como modelo de machine learning.
Função predict()
Talvez alguns tenham percebido que utilizamos a função predict() em alguns códigos apresentados. Esta função é utilizada para realizar previsões na linguagem R.
> predict(lm(altura ~ peso))
1 2 3 4 5 6 7 8
1.538911 1.576504 1.651690 1.614097 1.636653 1.621616 1.561467 1.599060
Se simplesmente passamos o modelo como parâmetro na função predict(), temos como retorno os valores de y, para os valores de x existentes. No caso, os valores das alturas previstas para os pesos apresentados, sendo os valores de 1 a 8 referentes as posições dos pesos na variável peso.
Esses são os valores utilizados no cálculo da soma dos quadrados dos erros da reta de regressão, conforme detalhamos anteriormente. Mas este não é o objetivo final. Queremos descobrir alturas de pessoas que só sabemos o peso, e para isso informaremos na função predict() estes pesos.
> pesos <- data.frame(peso = c(48, 51, 62))
> predict(lm(altura ~ peso), pesos)
1 2 3
1.561467 1.584023 1.666728
Agora passamos os pesos de pessoas que não estavam na base de dados utilizada para criação do modelo. A função predict() espera receber estes dados em um dataframe, por isso informamos desta forma.
Assim este simples modelo de machine learning prevê que uma pessoa com 48 quilos tenha 1.56 metros de altura, outra com 51, tenha 1.58, e com 62, 1.67.
Caso você queira conhecer a teoria necessária para se encontrar os coeficientes de uma reta por meio de gradiente descendente, confira abaixo a videoaula detalhada, com todos os cálculos necessários, explicados com muita didática:
Continue aprendendo
Um modelo de machine learning ainda possui outros pontos a serem considerados e analisados.
Focando principalmente na simplicidade e didática, montamos um curso de machine learning com linguagem R, que irá fornecer os primeiros passos para realmente compreender e dominar esta fascinante tecnologia.
Esse curso corresponde ao módulo I, que irá iniciar você no mundo do machine learning utilizando R, cobrindo algoritmos básicos como regressão linear, regressão logística, árvores de decisão, entre outros.
Já o módulo II cobre algoritmos mais avançados. Não deixe de conferir.
A linguagem R é uma excelente opção para criação de modelos de machine learning, por isso montamos também alguns cursos gratuitos super práticos e didáticos para você dominar os conceitos essenciais da linguagem, começando do zero:
Você pode conhecer todos os nossos cursos nessa página.
Leia também:
