Quando estamos trabalhando com estatística, existem alguns problemas que podem nos induzir ao erro por causa de “armadilhas intuitivas”. Nesses casos, é muito interessante utilizarmos o Teorema de Bayes, pois ele é capaz de nos livrar de tais armadilhas.
Você verá que esse teorema é importantíssimo nas áreas de machine learning e inteligência artificial podendo ser utilizado em diversos algoritmos.
Contexto para aplicação do Teorema de Bayes
Primeiramente, vamos a um exemplo de problema estatístico cuja maioria das pessoas tem uma tendência de errar. Imagine que temos um teste para detectar se pessoas têm uma doença ou não.
Imagine um teste que tem uma acurácia de 90% para qualquer um dos lados. O que isso significa?
Significa que, em 90% dos casos em que as pessoas que têm a doença e fazem esse teste, o resultado confirma a doença. Da mesma forma, se a pessoa não tem, o teste dirá, em 90% das vezes, que a pessoa não tem. Ou seja, o teste acerta em 90% das vezes.
Vamos supor que você, que está lendo este artigo, fez o teste e foi diagnosticado com a doença – o resultado do teste foi positivo. Então, a pergunta é: qual a probabilidade de você realmente ter essa doença?
Em um primeiro momento, a maioria das pessoas responderá que a chance de ter a doença é de 90%; afinal, a acurácia do teste é 90%!
Elas pensam: se o teste acerta 90% das vezes e ele diz que eu tenho, então há 90% de chance de eu realmente ter essa doença. Entretanto, esse pensamento está muito equivocado; o resultado verdadeiro está muito distante da resposta correta. Por quê?
Está faltando uma informação para que esse problema possa ser respondido: quantos por cento da população têm a doença em questão?
Em mais um cenário hipotético, imagine que 1% da população tenha, de fato, a doença. Nessa população, há 1000 pessoas; você, que foi diagnosticado com a doença, é uma dessas pessoas.
Se apenas 1% dessas pessoas têm a doença, então 10 pessoas têm e 990 não tem (1% de 1.000 é 10; 99% de 1.000 é 990). Dessas mil pessoas, todas farão o teste. Quais seriam os resultados nesse caso? Lembra-se que o teste acerta em 90% e erra em 10% das vezes. Confira na tabela abaixo.
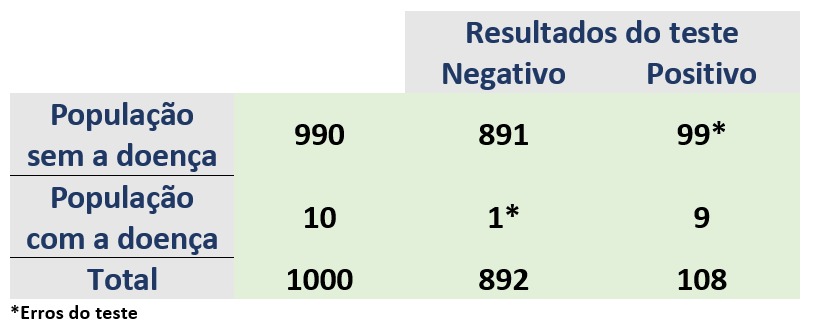
O teste diagnosticou 108 pessoas com a doença – resultado positivo; quantas pessoas, entretanto, tinham a doença? Apenas 9 pessoas. Então, qual é a probabilidade de se ter a doença? É 9 em 108, ou 8,33%, pois apenas 9 das 108 pessoas está, de fato, doente. Ou seja, o resultado é bem menor do que os 90% que geralmente as pessoas respondem intuitivamente.
Essa é a armadilha que comentamos anteriormente. Se você foi diagnosticado com a doença, nesse cenário, há só 8% de chance de você, realmente, estar doente. Anti-intuitivo, não é? E por quê isso? Porque uma parcela muito baixa da população (1%) tem a doença; isso faz toda a diferença.
Embora o teste tenha uma precisão alta – ele acerta em 90% dos casos –, ele erra em 10% das vezes. Como a nossa população que não está doente é grande, quando esse número é multiplicado pelo erro, por mais que seja um erro pequeno, há um número muito grande de falsos positivos.
O teste acaba dizendo que pessoas têm a doença sendo que elas não têm. Por isso, muitos pensam que a acurácia do teste é a probabilidade de se ter a doença.
O que temos que fazer é: descobrir quantos por cento da população tem a doença e, a partir disso, equacionar todo o problema com calma para descobrir qual é a chance real de uma pessoa estar doente. É esse processo que o teorema de Bayes fará por nós – ele equaciona todo o problema considerando as variáveis. E o melhor é que o teorema é genérico e pode ser utilizado em qualquer situação sem a necessidade de todo o raciocínio prévio que tivemos com o nosso exemplo.
Aplicando o teorema de Bayes
Agora, vamos utilizar o mesmo exemplo com a fórmula de Bayes. Depois podemos comparar os resultados para ver se eles são os mesmos. Abaixo, você pode ver a fórmula do teorema. Em seguida, explicamos o que cada parte significa.
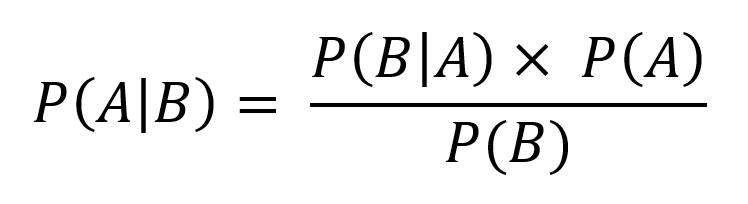
As letras A e B representam dois eventos distintos. No exemplo que estamos utilizando, um evento seria a probabilidade de estar doente e outro evento seria a probabilidade de o exame dar positivo. Note que nós poderíamos selecionar outros eventos, como a probabilidade de não se estar doente, ou ainda a probabilidade do teste dar negativo.
Entretanto, nós utilizamos o que interessa para nós, pois, como mencionamos anteriormente, no nosso exemplo, o exame deu positivo e queremos descobrir qual a probabilidade de se ter a doença. Por isso os eventos escolhidos foram esses.
A notação P(A|B) significa o seguinte: qual a probabilidade de ocorrer o evento A, dado que o evento B já ocorreu? Depois da barra (|), sempre colocaremos o evento que já ocorreu. Vamos dizer que, no nosso caso, A é a probabilidade de estar doente e B é a probabilidade de o exame dar positivo.
Assim, P(A|B) representa a probabilidade de estar doente (evento A) sendo que o exame deu positivo (evento B). Repare que é exatamente isso que queremos descobrir no nosso problema.
Nessa mesma lógica, P(B|A) representa a probabilidade de o exame dar positivo se é sabido que a pessoa está doente. Agora a pergunta é: se A já ocorreu, qual probabilidade de B ocorrer nesse cenário?
Note que isso é a própria acurácia do teste – para quem está doente, ele acerta 90% das vezes, ou a probabilidade de 0,9.
P(A) é simplesmente a probabilidade do evento A – a probabilidade de estar doente, que aqui, no nosso exemplo, é de 1%, ou 0,01.
Da mesma forma, P(B) é a probabilidade do evento B ocorrer – a probabilidade do teste dar positivo. Nós não temos essa informação diretamente, pois a probabilidade do teste dar positivo dependerá de a pessoa estar ou não doente.
Assim, teremos que equacionar a fórmula de uma maneira um pouco diferente, como podemos ver abaixo.
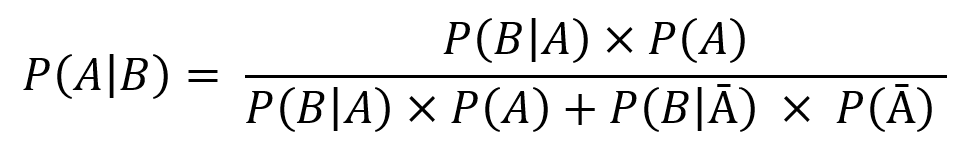
A probabilidade de B ocorrer pode ser escrita desta forma genérica: P(B│A) × P(A) + P(B│Ā) × P(Ā). Mas o que significa isso?
P(B│A) × P(A) representa a probabilidade do B ocorrer quando A ocorre;
P(B│Ā) × P(Ā) representa a probabilidade de B ocorrer quando A não ocorre.
Note que, para representarmos a probabilidade de um evento não ocorrer, colocamos um traço em cima do evento entre parênteses, como pode ser visto em P(Ā).
Em suma, a probabilidade de B ocorrer é a soma entre as probabilidades de B ocorrer quando o evento A ocorre e quando o evento A não ocorre.
Mas afinal, qual é a probabilidade de o exame dar positivo sendo que a pessoa não está doente? É o erro do teste. Se o teste acerta 90% das vezes, ele erra em 10%. Logo, temos que P(B│Ā) = 0,1.
Seguindo essa mesma lógica, qual é a probabilidade do evento A não ocorrer? Ou seja, qual a probabilidade de uma pessoa da população não estar doente?
Como havíamos mencionado anteriormente em nosso exemplo hipotético, apenas 1% da população apresenta a doença. Concluímos então que a probabilidade de não estar doente é de 99%. Logo, P(Ā) = 0,99.
Agora, como as incógnitas já foram explicadas e os dados discutidos, podemos colocar os números na fórmula. Confira abaixo:
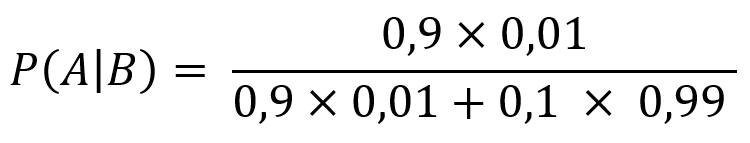
Calculando isso, chegaremos exatamente no mesmo resultado de antes: 0,083, ou 8,3%. Confira com sua calculadora.
É interessante observar que o Teorema de Bayes – quando ele já está equacionado – no numerador (parte de cima) ele está calculando a probabilidade de o teste dar positivo se a pessoa está doente; no denominador, ele está calculando a probabilidade de o teste dar positivo quando a pessoa está doente somada com a probabilidade de o teste dar positivo quando a pessoa não tem a doença.
Ou seja, o teorema está dividindo a probabilidade de o exame dar positivo se a pessoa está doente por todos os casos em que o teste dá positivo. Isso é exatamente o que havíamos feito anteriormente.
Assim, percebemos que o teorema de Bayes fará mais genericamente, com probabilidades, o que anteriormente havíamos feito considerando a quantidade de pessoas. Por isso, podemos aplicar o teste não importando a quantidade de pessoas que temos. Apenas precisamos saber as probabilidades.
Se você preferir, também pode conferir a explicação sobre o assunto na videoaula abaixo:
Aprofunde seu conhecimento
Agora que você aprendeu o que é o Teorema de Bayes, você pode continuar estudando sobre o assunto.
Recomendamos que você aprofunde seus conhecimentos em matemática, visto que isso é muito útil no aprendizado de Machine Learning e inteligência artificial; portanto, faça nosso curso gratuito de Matemática para Machine Learning.
Além disso, nos Cursos de Machine learning com Python, você verá outras aplicações para o teorema de Bayes e diversos outros conceitos importantíssimos, sempre de forma muito prática e didática. Não deixe de conferir!
Leia outros artigos:
- Percentil e quartil
- Conceitos de Variância e Viés
- Entenda o básico de probabilidade
- De onde vem o número de Euler
- O que são Algoritmos de Machine Learning
- Como funciona o algoritmo Árvore de Decisão
- Como funciona o algoritmo KNN
- Sistemas de Recomendação
- Redes Neurais e Deep Learning
- Gradiente Descendente e Regressão Linear
