Redes neurais em problemas de regressão

Cérebro conectado a uma rede Como já vimos anteriormente, existem vários tipos de redes neurais – convolucionais, recorrentes etc. Além disso, já aprendemos que existem diferentes tipos de problemas.

Até o momento, focamos mais em problemas de classificação; agora, entretanto, chegou a hora de falarmos de problemas de regressão, pois as redes neurais também podem ser utilizadas neles.

A boa notícia é que não vamos ter que aprender nenhuma teoria nova: não existe um formato de rede neural que sirva somente para um tipo de problema; diferentes tipos de redes neurais servem para problemas tanto de classificação quanto de regressão.

Na realidade, a diferença entre esses tipos de problemas é muito sutil – é só na última camada. Tudo o que vimos nos artigos mencionados acima continuará sendo válido para os problemas de regressão; trabalharemos com uma quantidade de features do nosso dataset igual à quantidade de neurônios de entrada; teremos que definir a quantidade de layers (camadas ocultas); faremos vários testes; utilizaremos algoritmos de otimização e funções de ativação.

A única diferença estará na camada de saída. Nessa camada, para problemas de classificação, a quantidade de neurônios que utilizávamos dependia da quantidade de classes que tínhamos.

Se tínhamos quatro classes em nosso problema, teríamos quatro neurônios de saída – um para cada classe; o neurônio que estivesse mais ativo seria a classe resultante para aquela amostra específica que havia entrado. Para problemas de regressão, será um pouco diferente: teremos apenas um neurônio de saída. Esse neurônio que nos dará a resposta final.

Apenas um neurônio de saída - problema de regressão

Aprofundando a diferença

A principal diferença dos problemas de regressão está na variável target. No target – ou variável y – para problemas de classificação, geralmente temos um valor para cada classe; quando fazemos one-hot-encoding criamos várias colunas de 0 ou 1 para identificar cada classe.

Analise o exemplo abaixo; nele, queremos classificar algumas maçãs conforme seus tipos. Há mais de uma saída possível, mas elas estão limitadas pelos tipos de maçãs (gala, fuji, argentina e verde); o número 1 representa que a maçã pertence àquele tipo; o número zero representa que ela não pertence ao tipo em questão.

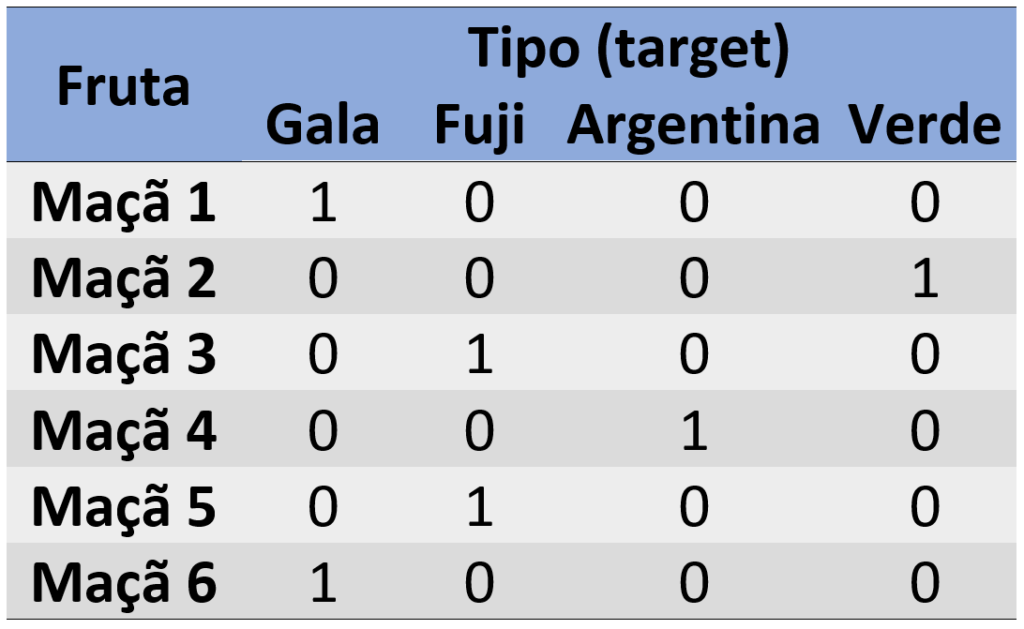
Tabela de problemas de classificação com um valor para cada classe

Para problemas de regressão, a nossa variável target – a variável y – é uma coluna só e ela possui valores diversos dentro de um range – os valores específicos dependerão do problema.

Se tivermos um dataset para prever preços de imóveis, por exemplo, teremos uma variação muito grande na saída; essa variação pode estar na casa das dezenas ou centenas de milhares, podendo chegar até a milhões de reais ou dólares. Haverá uma variação muito grande de preços que podem assumir qualquer valor no meio do caminho.

Ou seja, teremos muitas opções que estarão em uma coluna na variável target; cada linha é um desses valores e não uma classe específica.

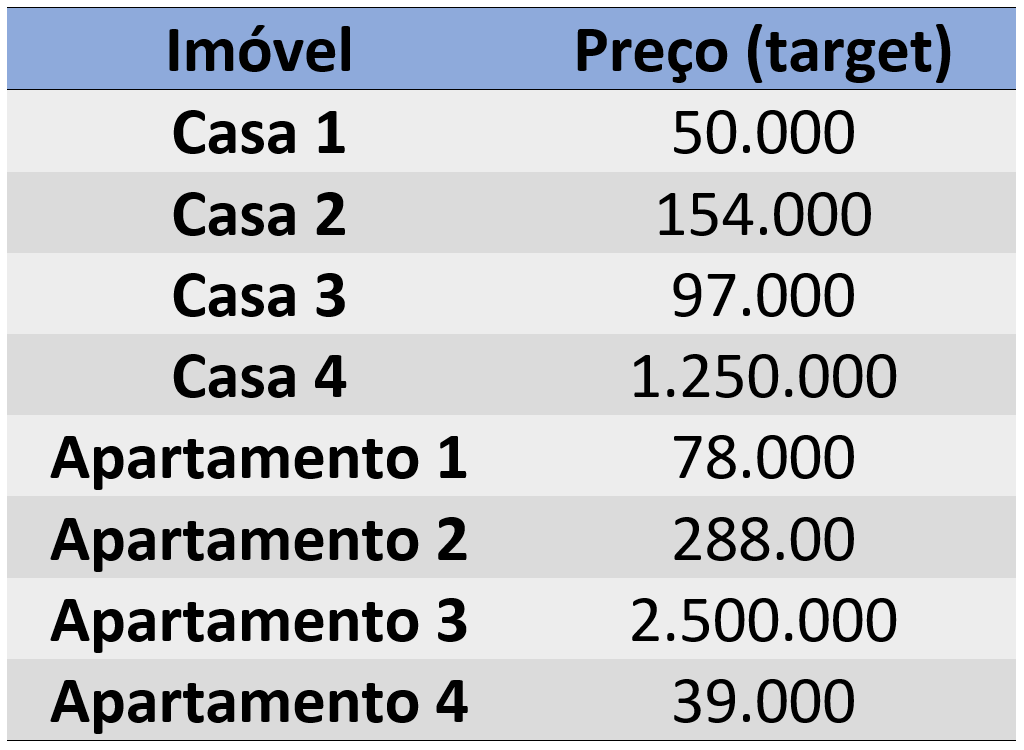
Problemas de regressão com valores que variam

Como visto anteriormente, quando temos um problema de regressão, teremos apenas um neurônio que dará a saída, que é um valor variável dentro desse grande range de valores possíveis.

Nesse caso, nosso neurônio de saída – a última camada – não terá uma função de ativação como a sigmoide ou a softmax, que são usadas para os problemas de classificação. Isso se dá pois tais funções limitam a saída em um range entre 0 e 1.

É justamente isso que não queremos; nós queremos que o nosso neurônio de saída nos dê uma resposta de qualquer valor. Afinal, se o nosso problema de regressão está prevendo o preço de imóveis, queremos que esses valores possam assumir qualquer ponto.

Por isso, não podemos limitar a nossa saída, em um problema de regressão, a uma faixa específica como é o caso dos problemas de classificação.

Além disso, apesar de não utilizar uma função de ativação, nosso neurônio responsável por dar as respostas será envolto por uma – a função linear, nesse caso.

Dependendo do problema de regressão do qual estivermos falando, o neurônio pode até assumir valores negativos como resposta final. E é exatamente isso que queremos: a possibilidade de nosso resultado ser qualquer valor, sem nenhum tipo de limite.

Por isso, não precisamos limitar nossa saída: ela pode ser uma função de ativação linear. Ou seja, a entrada será reproduzida exatamente igual na saída.

Podemos, entretanto, utilizar camadas de ativação, nas camadas intermediárias, da mesma forma que utilizávamos em problemas de classificação. Para cada camada intermediária podemos usar, por exemplo, a função ReLU ou a função sigmoide.

A única camada na qual não usaremos função de ativação – além da função linear – é a camada de saída que será o neurônio responsável por nos dar a resposta do problema de regressão.

Clips de papel sem organização - conceito de início caótico

É evidente que, no início, quando começarmos a treinar a rede neural, sem função de ativação e com pesos e bias aleatórios, a saída será muito caótica – terá valores muito grandes ou muito pequenos.

Na medida em que vamos treinando, entretanto, ela terá uma comparação para cada amostra. Vamos supor que, em nosso problema de previsão de preços de imóveis, o valor de saída deveria ser 56.357.

Nosso neurônio, no entanto, deu como resposta um valor completamente caótico (1.278.879); a função de custo, então, tentará se aproximar do valor previsto. Em uma próxima saída, pode ser que o resultado seja 130 mil, por exemplo.

Nesse caso, a função novamente comparará os valores e tentará reduzir o erro. E assim sucessivamente.

A cada resultado, o valor será comparado e haverá uma tentativa de se reduzir o erro.

Clips de papel organizados - conceito de convergência para a resposta certa

E assim será com cada uma das amostras. Se trabalharmos com lotes (batches), como no caso do gradiente descendente estocástico, cada lote terá seu resultado.

A função de custo tentará reduzir o erro para cada resultado se aproximando o máximo possível do valor exato, deixando a saída cada vez mais “organizada”.

Assim, ela trabalhará da mesma forma que em problemas de classificação.

Nós podemos também trabalhar com funções de custo diferentes das utilizadas em problemas de classificação. Não precisamos, por exemplo, utilizar função de entropia cruzada, pois a nossa saída não terá uma função sigmoide.

Como aprender mais

Gostou de conhecer mais sobre redes neurais e problemas de regressão? Então continue estudando o assunto com nossos cursos de Machine Learning e inteligência artificial com Python.

Você poderá aprofundar seus conhecimentos sobre redes neurais, além de aprender e aplicar outros conceitos muito importantes – como árvore de decisão, random forest, frameworks, algoritmos genéticos e muitos outros.

Além disso, temos outras opções de cursos, tanto pagos quanto gratuitos, para você que quer aprender cada vez mais sobre machine learning. Todos os nossos cursos são focados na didática e na compreensão do aluno. Clique aqui e confira!