Você já ouviu falar sobre quartil e percentil? Se não, você não precisa se assustar com esses nomes diferentes. Leia esse artigo até o final e você verá que esses conceitos são simples de serem compreendidos.
Além disso, esses conteúdos de matemática são essenciais para muitas áreas do machine learning. Então, não perca essa oportunidade de aprofundar seu conhecimento.
O que é percentil?
Percentil, como podemos perceber pelo nome, tem a ver com “por cento”. Para entendermos melhor o conceito, vamos imaginar que temos um conjunto de dados divididos em cem partes ordenadas da menor para a maior – cada uma dessas partes é um percentil.
Você pode imaginar isso aplicado em uma régua, por exemplo. Essa régua tem cem centímetros (ou um metro) e apresenta um risco a cada centímetro. Cada uma dessas divisões representará um percentil.
Então, quando nos referirmos ao décimo percentil de um conjunto de dados, estaremos falando de 10% dos dados, por exemplo; quando nos referirmos ao vigésimo percentil, estaremos falando de 20% dos dados; e assim por diante. Lembre-se entretanto, que não é simplesmente 10 ou 20% dos dados, mas 10 ou 20% dos menores dados, pois os dados estarão ordenados do menor ao maior.
Também pode ser comum você ouvir alguém falando que determinado valor não está contido no percentil 90, por exemplo. Isso quer dizer que esse valor não está entre os 90% menores valores; ou seja, ele está entre os 10% maiores valores. Percentil, então, refere-se sempre aos menores valores e determina um percentual ordenado destes valores.
Esse conceito é simples, mas pode ser compreendido melhor quando aplicado dentro do conceito de quartil.
O que é quartil?
O quartil nada mais é do que uma representação ou uma delimitação para o percentil. Na prática, teremos três quartis que dividirão um conjunto de dados em quatro partes iguais.
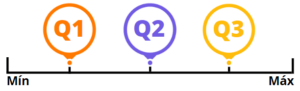
Imagine que esta imagem ao lado é nosso conjunto de dados com infinitos pontos ordenados do maior para o menor. Alguns pontos estão representados na imagem: o menor valor (Mín), o maior valor (Máx) e os três quartis (Q1, Q2 e Q3). Os quartis dividirão nossos dados em 4 partes iguais – cada uma contendo 25% dos dados. Note que do valor mínimo até Q1 (primeiro quartil) estão os 25% menores valores; ou seja, o percentil 25. Olhando de Q2 (quartil 2) até o mínimo, teremos os 50% menores valores, que é a mesma coisa que o percentil 50. Entre Q2 e Q3 (quartil 3), temos mais 25%; assim, Q3 representa o percentil 75 (75% menores valores). Por fim, entre Q3 e o valor máximo, temos mais 25% por cento dos dados – os 25% maiores valores, fechando os 100%.
Agora, com o conceito de quartil compreendido, podemos aplicá-lo em um exemplo prático.
Colocando em prática
Analise o conjunto de dados abaixo que representa as notas de 0 a 100 que nove alunos tiraram em uma prova:
![]()
A primeira coisa a ser feita para encontrar os quartis é ordenar esses valores do menor ao maior. Teremos o conjunto abaixo:
![]()
Como poderemos encontrar, então, os quartis? Como os números estão ordenados do menor ao maior, o mais fácil será começar pelo quartil 2 (Q2), que representa o percentil 50; ou seja, ele está bem na metade dos dados. Assim teremos Q2 = 33. Note que Q2 também representa a mediana, que é o número que está no meio de um conjunto de dados ordenados.
Agora que já encontramos o quartil 2 (Q2), é a partir do que sobrou do lado esquerdo que vamos encontrar o primeiro quartil (Q1). Entretanto, temos um número par de dados: 13, 17, 25, 28. Nesse caso, qual será a mediana? Será a média entre os dois valores do meio desse subconjunto: (17 + 25)/2 = 21. Dessa forma, Q1 = 25. Para descobrirmos o quartil 3 (Q3) faremos a mesma coisa, mas com o subconjunto do lado direito: 41, 65, 69, 72. Então, faremos a mediana desses valores que é a média de 65 e 69: 67. Assim, Q3 = 67.
Como você pode perceber, a forma de calcular quartis é bem simples. No entanto, ainda mais importante do que saber encontrar os valore é entender o que isso significa em um conjunto de dados. Lembre que, em nosso exemplo, estamos falando de notas de alunos. O que o ponto 21, que encontramos, significa nesse caso? Significa que até o valor 21 (Q1) estão agrupadas as 25% menores notas dos 9 alunos. Já, abaixo do valor 33 (Q2), estão agrupados as 50% menores notas; acima do 33, estão as 50% maiores notas. Por fim, até o ponto 67 (Q3) estão representadas as 75% menores notas da turma.
Em suma, os quartis são interessantes para termos uma ideia de como os dados estão distribuídos e tirarmos algumas conclusões sobre esses dados. Nesse nosso exemplo, podemos concluir que as notas desses alunos foram baixas pois, de 0 a 100, 75% dos alunos obtiveram notas abaixo de 67.
Continue estudando:
Nesse artigo, você leu sobre conceitos de matemática essenciais na área da inteligência artificial. Nós recomendamos que você aprofunde os seus conhecimentos de matemática, pois isso irá lhe ajudar nos próximos passos. Para isso, não deixe de conferir nosso curso grátis de fundamentos de matemática.
Além disso, os conceitos de percentil e quartil são importantes para a utilização e compreensão de diagramas de caixa (ou boxplot) que é uma ferramenta muito utilizada em machine learning.
Se você tem interesse em aprender mais sobre box plot e outros assuntos relacionados, confira nosso curso de machine learning com Python. Com nossos cursos você aprende com exemplos práticos e muita didática. Nosso foco é o aprendizado do aluno. Clique aqui e confira todas opções.